Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!

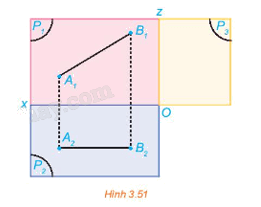
Hình 3.51 thể hiện hình chiếu đứng và hình chiếu bằng của một đoạn thẳng AB trong không gian.

Đề bài

Hình 3.51 thể hiện hình chiếu đứng và hình chiếu bằng của một đoạn thẳng AB trong không gian.

a) Xác định hình chiếu cạnh A₃B₃ của đoạn thẳng đó.

b) Biết A₁B₁ = 10 cm và A₂B₂ = 6 cm, tính độ dài của A₃B₃.

Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Quan sát hình 3.51 để tìm hình chiếu

Lời giải chi tiết

a) Hình chiếu cạnh của đoạn thẳng AB có hai đầu mút là hình chiếu cạnh A₃ của A và B₃ của B.

Để xác định A₃ ta làm như sau: Qua điểm A₂ vẽ đường thẳng vuông góc với Oz tại C và trên tia đối của tia Ox lấy điểm D sao cho OC = OD. Đường thẳng qua A₁ và vuông góc với Oz cắt đường thẳng qua D và vuông góc với Ox tại A₃. Tương tự xác định B₃. Nối A₃ và B₃ ta nhận được hình chiếu cạnh của đoạn thẳng AB.

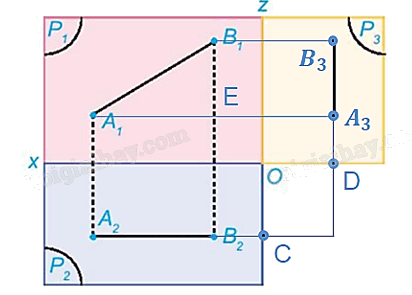
Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 3

b) Gọi E là giao điểm của A₁A₃ và B₁B₂.

Dễ dàng chứng minh tứ giác A₁A₂B₂E là hình chữ nhật.

Do đó: A₁E = A₂B₂.

Mà A₂B₂ = 6 cm nên A₁E = 6 cm.

Tam giác A₁B₁E vuông tại E nên \({A_1}{E^2}\; + {\rm{ }}{B_1}{E^2}\; = {\rm{ }}{A_1}{B_1}^2\;\) (định lí Pythagore)

Suy ra \({B_1}E = \sqrt {{A_1}{B_1}^2 - {A_1}{E^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) (cm).

Mà B₁E = A₃B₃ (A₃B₃B₁E là hình chữ nhật)

Vậy A₃B₃ = 8 cm.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng học toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần nắm vững các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm bậc nhất: Sử dụng các quy tắc đạo hàm để tìm đạo hàm f'(x).
Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng không.
Lập bảng biến thiên: Xác định dấu của đạo hàm trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến.
Kết luận về cực trị: Dựa vào bảng biến thiên để xác định các điểm cực đại, cực tiểu và giá trị tương ứng.

Lời giải chi tiết bài 3.21 trang 80

Đề bài: (Giả sử đề bài cụ thể của bài 3.21 được đưa ra ở đây. Ví dụ: Tìm cực đại, cực tiểu của hàm số y = x^3 - 3x^2 + 2)

Giải:

Tập xác định: Hàm số y = x^3 - 3x^2 + 2 có tập xác định là R.
Đạo hàm bậc nhất: y' = 3x^2 - 6x
Điểm dừng: Giải phương trình 3x^2 - 6x = 0, ta được x = 0 hoặc x = 2.
Bảng biến thiên:
x -∞ 0 2 +∞
y' + - +
y ↗ ↘ ↗
Kết luận: Hàm số đạt cực đại tại x = 0 với giá trị y = 2 và đạt cực tiểu tại x = 2 với giá trị y = -2.

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

Lưu ý khi giải bài tập về cực trị

Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
Sử dụng đúng các quy tắc đạo hàm để tránh sai sót.
Lập bảng biến thiên một cách cẩn thận để xác định chính xác khoảng đồng biến, nghịch biến và cực trị.
Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số hoặc sử dụng các công cụ tính toán trực tuyến.

Ứng dụng của việc tìm cực trị

Việc tìm cực trị của hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:

Tối ưu hóa: Tìm giá trị lớn nhất hoặc nhỏ nhất của một đại lượng nào đó.
Kinh tế: Xác định mức sản lượng tối ưu để đạt lợi nhuận cao nhất.
Kỹ thuật: Thiết kế các cấu trúc hoặc hệ thống có hiệu suất cao nhất.

Học toán online hiệu quả tại giaitoan.edu.vn

Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong các kỳ thi.