Bài 3.10 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh phải tính đạo hàm, tìm cực trị và vẽ đồ thị hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong HĐ7, bằng cách xét tam giác vuông OIA
Đề bài
Trong HĐ7, bằng cách xét tam giác vuông OIA và tính tỉ số \(\frac{{IA}}{{OA}}\) , chứng minh rằng trong phép chiếu trục đo vuông góc đều thì \(p = q = r = \frac{{\sqrt 6 }}{3}\).
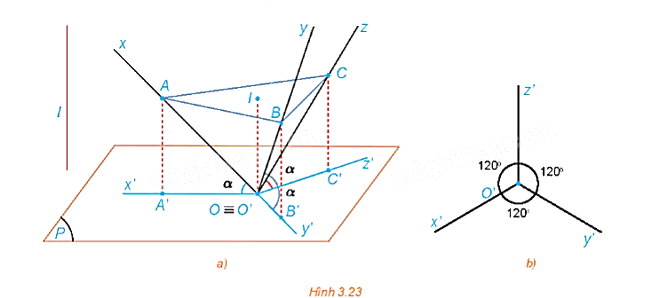
Phương pháp giải - Xem chi tiết
Các tỉ số \(p = \frac{{O'A'}}{{OA}},q = \frac{{O'B'}}{{OB}},r = \frac{{O'C'}}{{OC}}\) lần lượt là hệ số biến dạng theo trục \(O'x';\,\,O'y';\,\,O'z'\).
Lời giải chi tiết
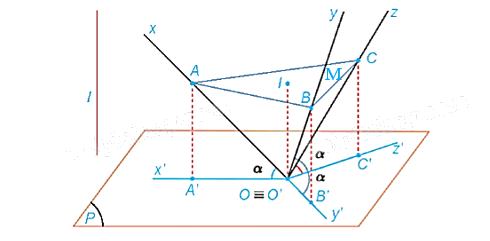
Gọi M là trung điểm của BC.
Ta có: O.ABC là hình chóp tam giác đều nên OA = OB = OC.
Vì I là tâm tam giác đều ABC nên . (1)
Tam giác OBC vuông cân tại O nên OM vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến.
Suy ra \(OM = \frac{1}{2}BC\) hay 2OM = BC.
Tam giác vuông cân OBC có \(2O{B^2}\; = {\rm{ }}B{C^2}.\)
Do đó: \(2O{B^2}\; = {\rm{ }}4O{M^2}\). Suy ra \(O{M^2}\; = \frac{1}{2}O{A^2}.{\rm{ }}\left( 2 \right)\)
Tam giác OIM vuông tại I có: \(O{I^2}\; + {\rm{ }}I{M^2}\; = {\rm{ }}O{M^2}.{\rm{ }}\left( 3 \right)\)
Mà \(O{I^2}\; = {\rm{ }}O{A^2}\;-{\rm{ }}I{A^2}\) (tam giác OIA vuông tại I) (4)
Thay (1), (2), (4) vào (3) ta được: \(O{A^2} - I{A^2} + \frac{1}{4}I{A^2} = \frac{1}{2}O{A^2}\)
Suy ra \(\frac{{I{A^2}}}{{O{A^2}}} = \frac{2}{3}\) nên \(\frac{{IA}}{{OA}} = \frac{{\sqrt 6 }}{3}\).
Mà IA = O'A' (do AIO'A' là hình bình hành).
Do đó, \(p = q = r = \frac{{O'A'}}{{OA}} = \frac{{\sqrt 6 }}{3}\).
Bài 3.10 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, bao gồm đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 3.10, yêu cầu thường là tìm đạo hàm của hàm số, tìm cực trị (cực đại, cực tiểu) của hàm số, và vẽ đồ thị hàm số. Việc xác định đúng yêu cầu của bài toán là bước đầu tiên quan trọng để giải quyết bài tập một cách chính xác.
Để tính đạo hàm của hàm số, học sinh cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, nếu hàm số là tổng của nhiều hàm số, đạo hàm của hàm số sẽ là tổng của đạo hàm của từng hàm số. Nếu hàm số là tích của hai hàm số, đạo hàm của hàm số sẽ được tính theo quy tắc tích. Việc nắm vững các quy tắc tính đạo hàm là yếu tố then chốt để giải quyết bài tập này.
Sau khi tính được đạo hàm của hàm số, học sinh cần tìm các điểm mà đạo hàm bằng 0 hoặc không xác định. Các điểm này là các điểm nghi ngờ là cực trị của hàm số. Để xác định xem một điểm nghi ngờ là cực đại hay cực tiểu, học sinh cần xét dấu của đạo hàm trong lân cận của điểm đó. Nếu đạo hàm đổi dấu từ dương sang âm, điểm đó là cực đại. Nếu đạo hàm đổi dấu từ âm sang dương, điểm đó là cực tiểu.
Sau khi tìm được cực trị của hàm số, học sinh có thể vẽ đồ thị hàm số. Để vẽ đồ thị hàm số, học sinh cần xác định các điểm đặc biệt của hàm số, bao gồm các điểm cắt trục, các điểm cực trị, và các điểm uốn. Sau đó, học sinh có thể vẽ đồ thị hàm số bằng cách nối các điểm này lại với nhau.
Giả sử hàm số cần xét là y = x3 - 3x2 + 2. Để giải bài tập này, ta thực hiện các bước sau:
Việc giải bài tập về đạo hàm và ứng dụng của đạo hàm có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tối ưu hóa các bài toán kinh tế, vật lý, và kỹ thuật. Ví dụ, trong kinh tế, đạo hàm có thể được sử dụng để tìm điểm tối ưu của hàm chi phí hoặc hàm doanh thu. Trong vật lý, đạo hàm có thể được sử dụng để tính vận tốc và gia tốc của một vật thể.
Bài 3.10 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các khái niệm và công thức liên quan, học sinh có thể giải quyết bài tập này một cách hiệu quả và áp dụng kiến thức vào các bài toán thực tế.