Bài 3.13 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp các em hiểu rõ hơn về kiến thức đã học.
Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 Kết nối tri thức đầy đủ, chính xác, giúp học sinh tự học hiệu quả và đạt kết quả cao trong các kỳ thi.
Đọc bản vẽ kĩ thuật trong Hình 3.48.
Đề bài
Đọc bản vẽ kĩ thuật trong Hình 3.48.
Phương pháp giải - Xem chi tiết
Khi đọc thông tin từ bản vẽ kĩ thuật ta tuân theo trình tự sau:
- Khung tên: xác định tên gọi của vật thể, vật liệu sử dụng để chế tạo vật thể, tỉ lệ bản vẽ.
- Hình biểu diễn: Xác định tên gọi của các hình chiếu có trong bản vẽ và các hình biểu diễn khác (nếu có).
- Kích thước: xác định kích thước chung của vật thể và kích thước cac thành phần.
- Yêu cầu kĩ thuật: xác định yêu cầu về gia công, xử lí bề mặt của vật thể.
Lời giải chi tiết
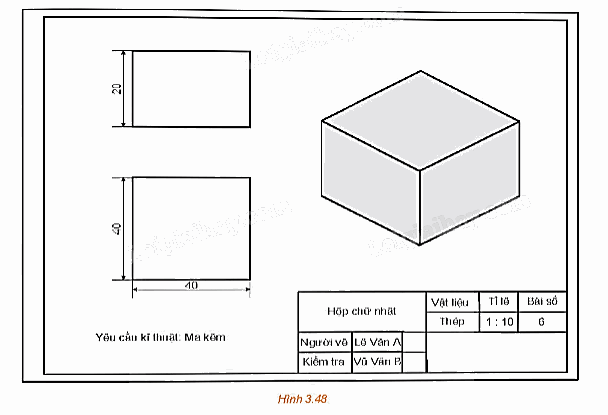
Bản vẽ kĩ thuật trong Hình 3.48 cho ta các nội dung sau:
- Khung tên:
+ Tên gọi vật thể: Hộp chữ nhật;
+ Vật liệu: Thép;
+ Tỉ lệ: 1 : 10.
- Hình biểu diễn:
+ Tên gọi hình chiếu: hình chiếu đứng, hình chiếu bằng, và hình chiếu trục đo vuông góc đều.
- Kích thước:
+ Vật thể có kích thước chung là: cao 20, ngang 40, dài 40.
- Yêu cầu kĩ thuật:
+ Xử lí bề mặt: Mạ kẽm.
Bài 3.13 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước tính toán, giải thích và kết luận. Ví dụ:)
Đề bài: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và vẽ đồ thị.
Giải:
Kết luận: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Việc giải bài 3.13 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng phân tích. Những kỹ năng này rất quan trọng trong học tập và trong cuộc sống.
Ngoài lời giải chi tiết trên giaitoan.edu.vn, học sinh có thể tham khảo thêm sách giáo khoa, sách bài tập, các trang web học toán online khác và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè để hiểu rõ hơn về bài toán này.
Để củng cố kiến thức và kỹ năng, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi làm bài kiểm tra và thi cử.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!