Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
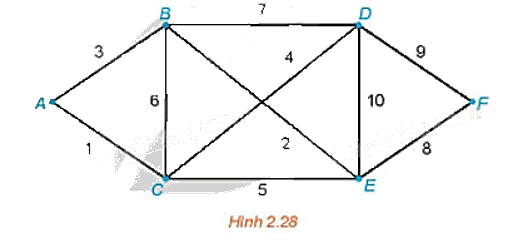
Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình.
Đề bài
Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình.
a) Hãy chỉ ra 2 đường đi từ A đến F và so sánh độ dài của hai đường đi đó.
b) Với mỗi đỉnh V của sơ đồ trên Hình 2.28, ta gắn số I(V) là khoảng cách ngắn nhất để đi từ A đến V và gọi là nhãn vĩnh viễn của đỉnh V. Như vậy, ta có ngay I(A) = 0. Dựa vào Hình 2.28, hãy tìm các nhãn vĩnh viễn I(B), I(C) của hai đỉnh kề với A là B, C.
Phương pháp giải - Xem chi tiết
Quan sát hình 2.28 để trả lời
Lời giải chi tiết
a) Hai đường đi từ A đến F, chẳng hạn là ABEF và ACEF.
Độ dài của đường đi ABEF là AB + BE + EF = 3 + 2 + 8 = 13.
Độ dài của đường đi ACEF là AC + CE + EF = 1 + 5 + 8 = 14.
Do đó, đường đi ABEF có độ dài ngắn hơn đường đi ACEF.
b) I(B) và I(C) lần lượt là các khoảng cách ngắn nhất để đi từ A đến B và C.
Ta có I(B) = AB = 3, I(C) = AC = 1.
Mục 1 trang 46 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một phần kiến thức cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Để giải quyết hiệu quả các bài toán trong mục này, học sinh cần hiểu rõ các khái niệm, định lý và công thức liên quan.
Để cung cấp một lời giải chi tiết, chúng ta cần xem xét từng bài tập cụ thể trong mục 1 trang 46. Tuy nhiên, dựa trên cấu trúc chung của Chuyên đề học tập Toán 11 - Kết nối tri thức, chúng ta có thể dự đoán các dạng bài tập thường gặp và phương pháp giải tương ứng.
Các bài tập thuộc dạng này thường yêu cầu học sinh:
Phương pháp giải:
Các bài tập thuộc dạng này thường yêu cầu học sinh:
Phương pháp giải:
Bài tập: (Giả sử đây là một bài tập cụ thể từ mục 1 trang 46)
Lời giải:
...
Ngoài sách giáo khoa và sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau:
Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức đòi hỏi sự nắm vững kiến thức lý thuyết và kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng mà giaitoan.edu.vn cung cấp, các bạn học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.