Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 1 trang 53, 54 của Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
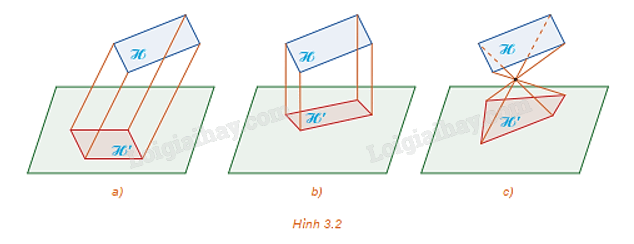
Hình 3.2 mô tả ba phép chiếu biến hình ℋ thành hình ℋ '.
Hình 3.2 mô tả ba phép chiếu biến hình ℋ thành hình ℋ '. Em đã biết những phép chiếu nào trong ba phép chiếu đó? Hãy nhắc lại khái niệm về các phép chiếu mà em đã học.
Phương pháp giải:
Quan sát hình vẽ, dựa vào kiến thức đã học để làm
Lời giải chi tiết:
Hình 3.2a sử dụng phép chiếu song song. Phép chiếu song song là phép chiếu có các tia chiếu song song với nhau nhưng không vuông góc với mặt phẳng chiếu.
Hình 3.2b sử dụng phép chiếu vuông góc. Phép chiếu vuông góc là phép chiếu có các tia chiếu vuông góc với mặt phẳng chiếu.
Hình 3.2c sử dụng phép chiếu xuyên tâm. Phép chiếu xuyên tâm là phép chiếu có các tia chiếu xuất phát tại một điểm (điểm này gọi là tâm chiếu).
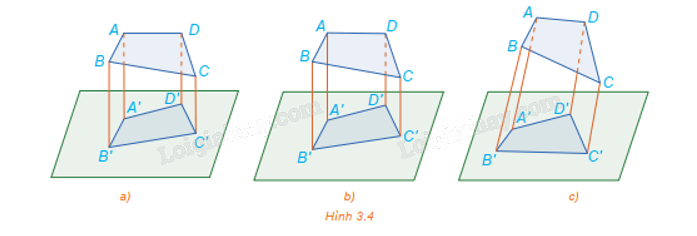
Quan sát Hình 3.4 và cho biết hình nào thể hiện hình chiếu trục đo của tứ giác ABCD.
Phương pháp giải:
Hình biểu diễn H’ của một hình, khối H trong không gian là hình chiếu của H lên mặt phẳng qua một phép chiếu. Nếu phép chiếu là phép chiếu song song thì H’ là hình chiếu trục đo của H.
Lời giải chi tiết:
Hình 3.4c có các đường thẳng AA', BB', CC', DD' đôi một song song nhưng không vuông góc với mặt phẳng chiếu nên Hình 3.4c thể hiện hình chiếu trục đo của tứ giác ABCD.
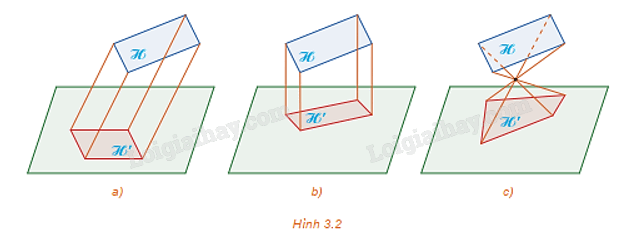
Hình 3.2 mô tả ba phép chiếu biến hình ℋ thành hình ℋ '. Em đã biết những phép chiếu nào trong ba phép chiếu đó? Hãy nhắc lại khái niệm về các phép chiếu mà em đã học.
Phương pháp giải:
Quan sát hình vẽ, dựa vào kiến thức đã học để làm
Lời giải chi tiết:
Hình 3.2a sử dụng phép chiếu song song. Phép chiếu song song là phép chiếu có các tia chiếu song song với nhau nhưng không vuông góc với mặt phẳng chiếu.
Hình 3.2b sử dụng phép chiếu vuông góc. Phép chiếu vuông góc là phép chiếu có các tia chiếu vuông góc với mặt phẳng chiếu.
Hình 3.2c sử dụng phép chiếu xuyên tâm. Phép chiếu xuyên tâm là phép chiếu có các tia chiếu xuất phát tại một điểm (điểm này gọi là tâm chiếu).
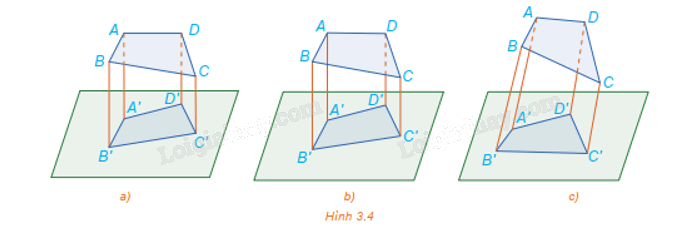
Quan sát Hình 3.4 và cho biết hình nào thể hiện hình chiếu trục đo của tứ giác ABCD.
Phương pháp giải:
Hình biểu diễn H’ của một hình, khối H trong không gian là hình chiếu của H lên mặt phẳng qua một phép chiếu. Nếu phép chiếu là phép chiếu song song thì H’ là hình chiếu trục đo của H.
Lời giải chi tiết:
Hình 3.4c có các đường thẳng AA', BB', CC', DD' đôi một song song nhưng không vuông góc với mặt phẳng chiếu nên Hình 3.4c thể hiện hình chiếu trục đo của tứ giác ABCD.
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng vào giải quyết các bài toán thực tế. Việc giải các bài tập trang 53 và 54 là bước quan trọng để củng cố kiến thức và đánh giá khả năng hiểu bài của học sinh.
Để giải quyết hiệu quả các bài tập trong mục này, trước tiên học sinh cần nắm vững các khái niệm và định lý liên quan. Thông thường, mục 1 sẽ đề cập đến:
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong trang 53. Lưu ý rằng, mỗi bài tập có thể yêu cầu áp dụng các kiến thức và kỹ năng khác nhau. Do đó, học sinh cần đọc kỹ đề bài, xác định đúng yêu cầu và lựa chọn phương pháp giải phù hợp.
Đề bài: Cho hàm số y = f(x) = x2 - 2x + 1. Tìm tập xác định và tập giá trị của hàm số.
Lời giải:
Đề bài: Giải phương trình: 2x + 3 = 7
Lời giải:
2x = 7 - 3
2x = 4
x = 2
Tương tự như trang 53, chúng ta sẽ giải chi tiết từng bài tập trong trang 54. Các bài tập ở trang này có thể có độ khó cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và tư duy logic.
Đề bài: Tìm đạo hàm của hàm số y = x3 + 2x2 - 5x + 1.
Lời giải:
y' = 3x2 + 4x - 5
Đề bài: Tính tích phân ∫(x2 + 1) dx
Lời giải:
∫(x2 + 1) dx = (x3/3) + x + C
Việc giải các bài tập trong mục 1 trang 53, 54 Chuyên đề học tập Toán 11 - Kết nối tri thức là một quá trình quan trọng để củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng rằng, với hướng dẫn chi tiết và các mẹo học tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc chinh phục môn Toán.