Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11.
Chúng tôi tập trung vào việc giúp học sinh nắm vững kiến thức và kỹ năng giải toán thông qua các bài giảng và bài tập được trình bày một cách rõ ràng, logic.
Bài viết này sẽ cung cấp đáp án và phương pháp giải cho mục 3 trang 38, 39, 40 trong Chuyên đề học tập Toán 11 - Kết nối tri thức, giúp bạn tự tin hơn trong quá trình học tập.
Cho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua)
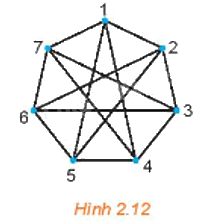
Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối đỉnh 1 và đỉnh 6.
Phương pháp giải:
Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Lời giải chi tiết:
Đồ thị Hình 2.12 có 7 đỉnh, lấy 2 đỉnh bất kì của đồ thị, ta đều thấy có một đường đi nối hai điểm đó, do đó mọi cặp đỉnh của đồ thị này đều liên thông nên đồ thị này liên thông.
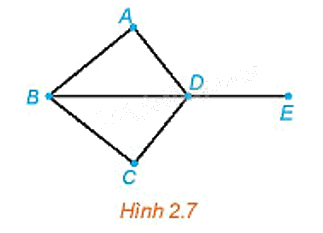
Cho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:
a) Đi từ đỉnh A đến đỉnh E.
b) Đi từ đỉnh A và lại quay về đỉnh A.
Phương pháp giải:
Quan sát hình 2.7 để làm
Lời giải chi tiết:
a) Để đi từ đỉnh A đến đỉnh E ta có thể di chuyển theo con đường từ A đến D rồi từ D đến E (hoặc cũng có thể chọn các con đường khác, chẳng hạn đi theo đường từ A đến B rồi từ B đến D và từ D đến E, ...)
b) Để đi từ đỉnh A và lại quay về đỉnh A ta có thể di chuyển theo con đường từ A đến D rồi từ D đến B và từ B quay lại A (tương tự cũng có thể chọn các con đường khác).
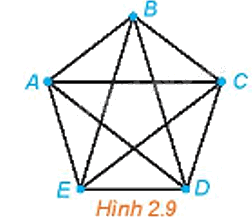
Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có: độ dài 4; độ dài 5.
Phương pháp giải:
Một đường đi (chu trình) qua n cạnh gọi là một đường đi (chu trình) có độ dài n.
Lời giải chi tiết:
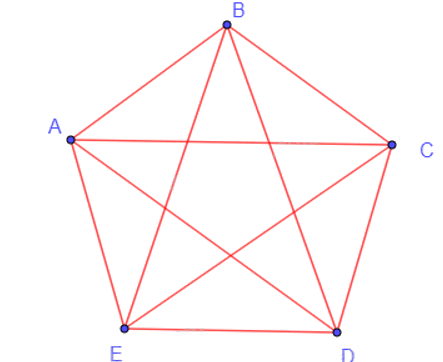
Những chu trình sơ cấp có độ dài 4 xuất phát từ đỉnh A là: ABCDA, ABCEA, ABDCA, ABDEA, ABEDA, ABECA, ACBDA, ACBEA, ACDBA, ACDEA, ACEBA, ACEDA, ADBEA, ADBCA, ADCEA, ADCBA, ADEBA, ADECA, AEBDA, AEBCA, AECDA, AEDCA, AECBA, AEDBA.
Những chu trình sơ cấp có độ dài 5 xuất phát từ đỉnh A là: ABCDEA, ABCEDA, ABECDA, ABEDCA, ABDCEA, ABDECA, ACBEDA, ACBDEA, ACDEBA, ACDBEA, ACEDBA, ACEBDA, ADBECA, ADBCEA, ADCBEA, ADCEBA, ADECBA, ADEBCA, AECDBA, AECBDA, AEDCBA, AEDBCA, AEBCDA, AEBDCA.
Nhận biết tính liên thông của đồ thị
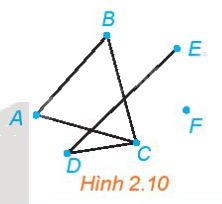
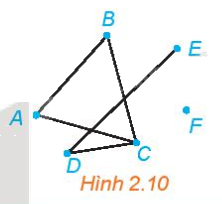
Trong đồ thị ở Hình 2.10, hãy:
a) Tìm một đường đi từ đỉnh A đến đỉnh E.
b) Có tồn tại một đường đi từ đỉnh A đến đỉnh F hay không?
Phương pháp giải:
Quan sát hình 2.10 để trả lời
Lời giải chi tiết:
a) Một đường đi từ đỉnh A đến đỉnh E là: ABCDE.
b) Không tồn tại đường đi nào từ đỉnh A đến đỉnh F vì F là đỉnh cô lập.
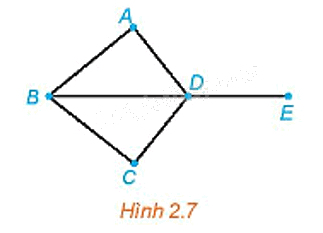
Cho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:
a) Đi từ đỉnh A đến đỉnh E.
b) Đi từ đỉnh A và lại quay về đỉnh A.
Phương pháp giải:
Quan sát hình 2.7 để làm
Lời giải chi tiết:
a) Để đi từ đỉnh A đến đỉnh E ta có thể di chuyển theo con đường từ A đến D rồi từ D đến E (hoặc cũng có thể chọn các con đường khác, chẳng hạn đi theo đường từ A đến B rồi từ B đến D và từ D đến E, ...)
b) Để đi từ đỉnh A và lại quay về đỉnh A ta có thể di chuyển theo con đường từ A đến D rồi từ D đến B và từ B quay lại A (tương tự cũng có thể chọn các con đường khác).
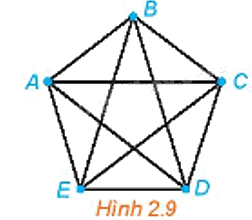
Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có: độ dài 4; độ dài 5.
Phương pháp giải:
Một đường đi (chu trình) qua n cạnh gọi là một đường đi (chu trình) có độ dài n.
Lời giải chi tiết:
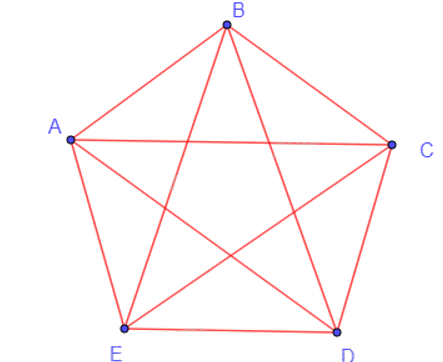
Những chu trình sơ cấp có độ dài 4 xuất phát từ đỉnh A là: ABCDA, ABCEA, ABDCA, ABDEA, ABEDA, ABECA, ACBDA, ACBEA, ACDBA, ACDEA, ACEBA, ACEDA, ADBEA, ADBCA, ADCEA, ADCBA, ADEBA, ADECA, AEBDA, AEBCA, AECDA, AEDCA, AECBA, AEDBA.
Những chu trình sơ cấp có độ dài 5 xuất phát từ đỉnh A là: ABCDEA, ABCEDA, ABECDA, ABEDCA, ABDCEA, ABDECA, ACBEDA, ACBDEA, ACDEBA, ACDBEA, ACEDBA, ACEBDA, ADBECA, ADBCEA, ADCBEA, ADCEBA, ADECBA, ADEBCA, AECDBA, AECBDA, AEDCBA, AEDBCA, AEBCDA, AEBDCA.
Nhận biết tính liên thông của đồ thị
Trong đồ thị ở Hình 2.10, hãy:
a) Tìm một đường đi từ đỉnh A đến đỉnh E.
b) Có tồn tại một đường đi từ đỉnh A đến đỉnh F hay không?
Phương pháp giải:
Quan sát hình 2.10 để trả lời
Lời giải chi tiết:
a) Một đường đi từ đỉnh A đến đỉnh E là: ABCDE.
b) Không tồn tại đường đi nào từ đỉnh A đến đỉnh F vì F là đỉnh cô lập.
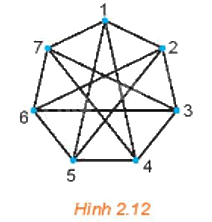
Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối đỉnh 1 và đỉnh 6.
Phương pháp giải:
Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Lời giải chi tiết:
Đồ thị Hình 2.12 có 7 đỉnh, lấy 2 đỉnh bất kì của đồ thị, ta đều thấy có một đường đi nối hai điểm đó, do đó mọi cặp đỉnh của đồ thị này đều liên thông nên đồ thị này liên thông.
Mục 3 của Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Mục 3 bao gồm các nội dung chính sau:
Trang 38 chứa các bài tập về việc tính đạo hàm của hàm số tại một điểm. Để giải các bài tập này, học sinh cần nắm vững định nghĩa đạo hàm và quy tắc tính đạo hàm của tổng, hiệu, tích, thương của hai hàm số.
Ví dụ, bài tập 1 yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x tại điểm x = 1. Ta có:
f'(x) = 2x + 2
f'(1) = 2(1) + 2 = 4
Vậy đạo hàm của hàm số f(x) tại điểm x = 1 là 4.
Trang 39 chứa các bài tập về việc tính đạo hàm của các hàm số cơ bản. Để giải các bài tập này, học sinh cần nắm vững quy tắc tính đạo hàm của các hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit.
Ví dụ, bài tập 2 yêu cầu tính đạo hàm của hàm số f(x) = sin(x). Ta có:
f'(x) = cos(x)
Trang 40 chứa các bài tập về ứng dụng của đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số. Để giải các bài tập này, học sinh cần nắm vững các kiến thức về đạo hàm và ứng dụng của đạo hàm.
Ví dụ, bài tập 3 yêu cầu tìm phương trình tiếp tuyến của đồ thị hàm số f(x) = x2 tại điểm x = 2. Ta có:
f'(x) = 2x
f'(2) = 2(2) = 4
f(2) = 22 = 4
Phương trình tiếp tuyến của đồ thị hàm số f(x) tại điểm x = 2 là:
y - 4 = 4(x - 2)
y = 4x - 4
Để học tốt Mục 3, bạn nên:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải các bài tập trong Mục 3 trang 38, 39, 40 Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc bạn học tập tốt!