Bài 2.26 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp bạn hiểu rõ hơn về kiến thức đã học.
Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 Kết nối tri thức đầy đủ, chính xác, giúp bạn tự học hiệu quả và đạt kết quả cao trong các kỳ thi.
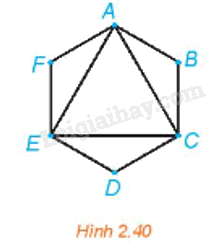
Tìm một chu trình Euler trong đồ thị trên Hình 2.40.
Đề bài
Tìm một chu trình Euler trong đồ thị trên Hình 2.40.
Phương pháp giải - Xem chi tiết
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết
Ta thấy đồ thị Hình 2.40 liên thông và mọi đỉnh của đồ thị này đều có bậc chẵn nên theo định lí Euler thì đồ thị này có một chu trình Euler.
Một chu trình Euler trong đồ thị trên Hình 2.40 là ABCDEFAECA.
Bài 2.26 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc khảo sát hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Cho hàm số y = x3 - 3x2 + 2. Khảo sát hàm số.)
Giải:
Hàm số y = x3 - 3x2 + 2 xác định trên tập số thực R.
y' = 3x2 - 6x
y'' = 6x - 6
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Vậy hàm số có hai điểm cực trị: x1 = 0 và x2 = 2
Giải phương trình y'' = 0:
6x - 6 = 0
=> x = 1
Vậy hàm số có điểm uốn tại x = 1
Hàm số y = x3 - 3x2 + 2 có:
Đồ thị hàm số có dạng:
(Mô tả đồ thị hàm số)
Bài toán khảo sát hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, như:
Việc nắm vững phương pháp giải bài toán khảo sát hàm số là rất quan trọng đối với học sinh lớp 11, giúp các em có nền tảng vững chắc để học tập các môn học khác và giải quyết các bài toán thực tế.