Bài 3.16 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp bạn hiểu rõ hơn về kiến thức đã học.
Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 Kết nối tri thức đầy đủ, chính xác, giúp bạn tự học hiệu quả và đạt kết quả cao trong các kỳ thi.
Hãy chọn một vật thể đơn giản theo ý thích của mình và lập bản vẽ kĩ thuật cho vật thể đó.
Đề bài
Hãy chọn một vật thể đơn giản theo ý thích của mình và lập bản vẽ kĩ thuật cho vật thể đó.
Phương pháp giải - Xem chi tiết
HS chọn bản vẽ theo ý thích để lập bản vẽ kĩ thuật
Khi lập bản vẽ kĩ thuật ta thực hiện theo các bước sau:
Bước 1: Quan sát vật thể và phân tích vật thể thành các hình khối đơn giản.
Bước 2: Chọn cac hướng chiếu phù hợp, thường là các hướng vuông góc với các mặt của vật thể.
Bước 3: Vẽ hình chiếu vuông góc của các hình khối cấu tạo nên vật thể.
Bước 4: Xóa cac nét thừa, chỉnh sửa các nét vẽ theo đúng tiêu chuẩn và ghi kích thước trên các hình chiếu.
Bước 5: Từ ba hình chiếu vuông góc vừa vẽ, vẽ hình chiếu trục đo vuông góc đều của vật thể.
Bước 6: Kẻ khung bản vẽ, khung tên, ghi các nội dung vào khung tên để hoàn thành bản vẽ.
Lời giải chi tiết
Chọn vật thể hộp chữ nhật rỗng giữa. Quy ước mỗi cạnh của tam giác đều có chiều dài 1 cm.
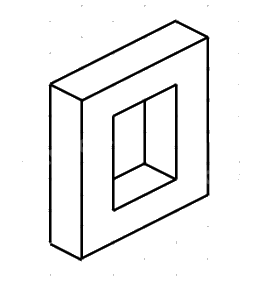
Lập bản vẽ kĩ thuật:
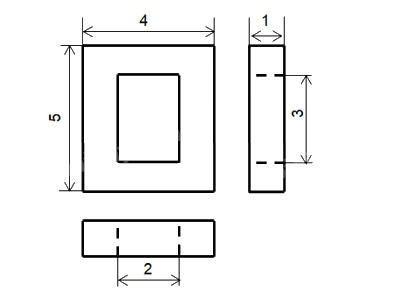
Bước 1: Nhận thấy rằng vật thể có dạng khối hộp chữ nhật rỗng được bao bởi một hình hộp chữ nhật, phần rãnh cũng là hình hộp chữ nhật.
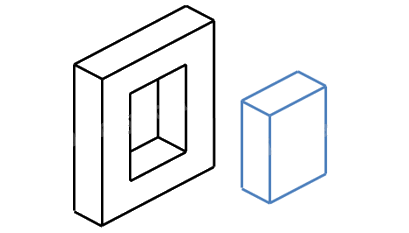
Bước 2: Chọn các hướng chiếu lần lượt vuông góc với mặt trước, mặt trên và mặt bên trái của vật thể.
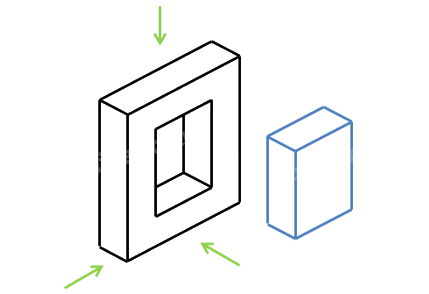
Bước 3: Lần lượt vẽ hình chiếu vuông góc của hình hộp chữ nhật bao bên ngoài vật thể, của khối hộp chữ nhật rỗng và của rãnh hộp chữ nhật.
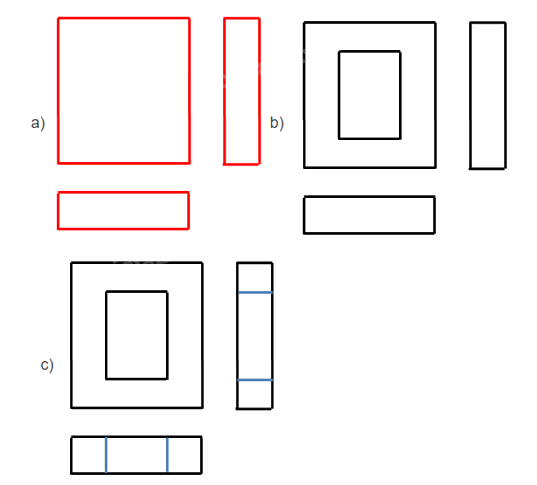
Bước 4: Xóa các nét thừa, chỉnh sửa các nét vẽ theo quy tắc: các đường thấy vẽ bằng nét liền; các đường khuất vẽ bằng nét đứt. Ghi các kích thước của vật thể trên các hình chiếu.
Bước 5: Vẽ hình chiếu trục đo vuông góc đều của vật thể.
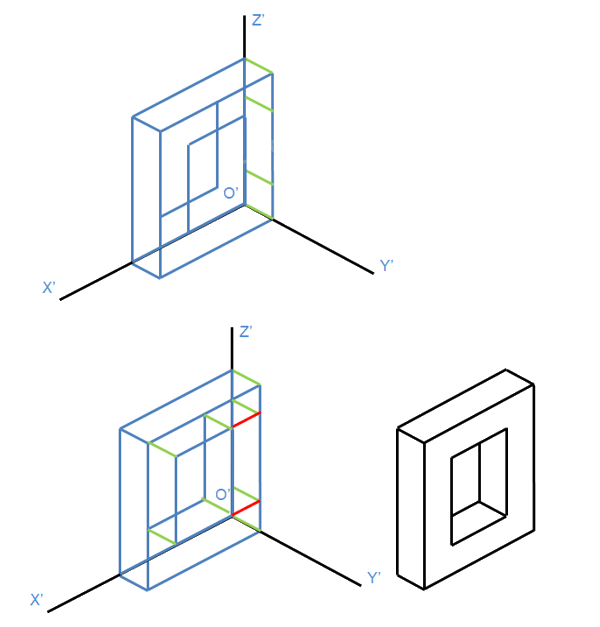
Bước 6: Hoàn thành khung tên, khung bản vẽ để được bản vẽ cuối cùng có dạng như sau:
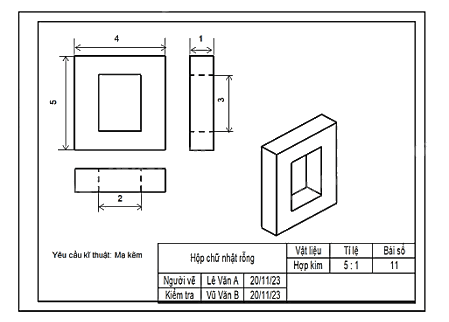
Bài 3.16 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm đạo hàm và sử dụng đạo hàm để khảo sát hàm số. Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài toán: (Giả sử bài toán cụ thể là: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm đạo hàm f'(x) và xác định các điểm cực trị của hàm số.)
Bước 1: Tính đạo hàm f'(x)
Sử dụng quy tắc tính đạo hàm của hàm số đa thức, ta có:
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Xác định loại điểm cực trị
Ta xét dấu của f'(x) trên các khoảng xác định:
Từ đó, ta kết luận:
Vậy, hàm số y = x3 - 3x2 + 2 đạt cực đại tại điểm (0, 2) và đạt cực tiểu tại điểm (2, -2).
Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc khảo sát hàm số, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Ngoài ra, bạn có thể sử dụng các công cụ tính đạo hàm online để kiểm tra lại kết quả của mình và tiết kiệm thời gian.
Khi giải các bài toán về đạo hàm, bạn cần chú ý đến các quy tắc tính đạo hàm và các điều kiện để hàm số có đạo hàm. Việc hiểu rõ các khái niệm cơ bản và áp dụng đúng các quy tắc sẽ giúp bạn tránh được các lỗi sai không đáng có.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!