Chào mừng các em học sinh đến với lời giải chi tiết bài 2.1 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác và đầy đủ.
Vẽ hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh
Đề bài
Vẽ hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh E(G) = {12; 14; 23; 25; 34; 35}.
Đồ thị G có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
Phương pháp giải - Xem chi tiết
- Một đồ thị không có khuyên, trong đó hai đỉnh được nối bằng nhiều nhất một cạnh (không có hai cạnh nào cùng nối một cặp đỉnh) gọi là một đơn đồ thị.
- Một đồ thị là đầy đủ khi và chỉ khi mỗi cặp đỉnh của nó đều được nối bằng một cạnh.
Lời giải chi tiết
Hình biểu diễn của đồ thị G như sau.
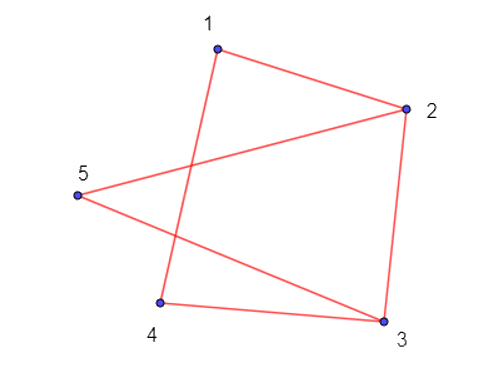
Đồ thị G là đơn đồ thị, nhưng không phải đồ thị đầy đủ.
Bài 2.1 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về dãy số, cấp số cộng, cấp số nhân vào giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa, tính chất của các loại dãy số và các công thức liên quan.
Bài tập 2.1 thường bao gồm các dạng bài sau:
Để giải bài tập 2.1 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức một cách hiệu quả, các em cần:
(Giả sử bài tập 2.1 có nội dung cụ thể như sau: Cho dãy số (un) với u1 = 2 và un+1 = 2un - 1. Tìm số hạng thứ 5 của dãy số.)
Lời giải:
Ta có:
Vậy số hạng thứ 5 của dãy số là u5 = 17.
(Ví dụ về một bài tập tương tự và lời giải chi tiết)
Các em có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về dãy số:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập 2.1 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức, các em sẽ tự tin hơn trong quá trình học tập môn Toán. Chúc các em học tốt!