Bài 1.22 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
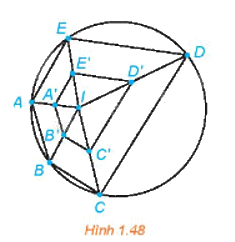
Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
Đề bài
Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
Phương pháp giải - Xem chi tiết
Quan sát hình 1.48 và dựa vào kiến thức về phép vị tự: Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
Vì A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE nên ta suy ra \(\overrightarrow {IA'} = \frac{1}{2}\overrightarrow {IA} ;\,\overrightarrow {IB'} = \frac{1}{2}\overrightarrow {IB} ;\,\overrightarrow {IC'} = \frac{1}{2}\overrightarrow {IC} ;\,\overrightarrow {ID'} = \frac{1}{2}\overrightarrow {ID} ;\,\,\overrightarrow {IE'} = \frac{1}{2}\overrightarrow {IE} \). Do đó, A', B', C', D', E' tương ứng là ảnh của các điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số \(\frac{1}{2}\).
Từ Hình 1.48, ta thấy các điểm A, B, C, D, E cùng thuộc một đường tròn. Vậy các điểm A', B', C', D', E' đều cùng thuộc một đường tròn là ảnh của đường tròn đi qua 5 điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số \(\frac{1}{2}\).
Bài 1.22 trang 29 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như đạo hàm, cực trị, và khoảng đơn điệu của hàm số.
Bài tập 1.22 thường có dạng yêu cầu học sinh:
Để giải bài 1.22 trang 29, ta thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta sẽ áp dụng các bước trên để giải bài tập:
Để giải bài tập 1.22 trang 29 hiệu quả, bạn nên:
Việc giải bài tập 1.22 trang 29 không chỉ giúp bạn hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic, và khả năng phân tích. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong nhiều lĩnh vực khác của cuộc sống.
Bài 1.22 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng và hữu ích. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.