Bài 1.23 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chương trình. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Quan sát ba hình được tô màu ở Hình 1.49, hình nhỏ nào là ảnh của hình lớn qua một phép vị tự?
Đề bài
Quan sát ba hình được tô màu ở Hình 1.49, hình nhỏ nào là ảnh của hình lớn qua một phép vị tự?
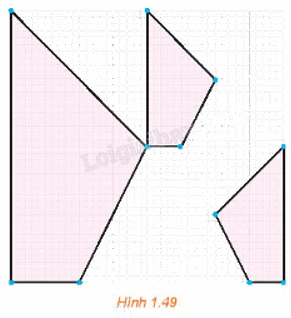
Phương pháp giải - Xem chi tiết
Quan sát hình 1.48 và dựa vào kiến thức về phép vị tự: Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
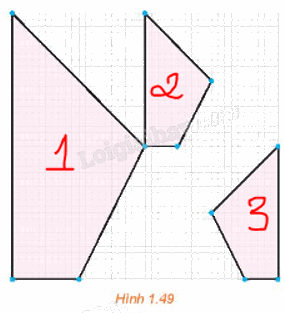
Hình nhỏ 2 là ảnh của hình lớn qua một phép vị tự.
Bài 1.23 trang 29 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải bài này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và cách vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Đề bài thường yêu cầu tìm tập xác định, tập giá trị, khoảng đồng biến, khoảng nghịch biến, điểm cực đại, điểm cực tiểu, hoặc vẽ đồ thị hàm số. Việc xác định đúng yêu cầu là bước đầu tiên quan trọng để giải bài thành công.
Để giải bài 1.23 trang 29, học sinh có thể áp dụng các phương pháp sau:
(Giả sử hàm số trong bài là y = f(x). Phần này sẽ trình bày lời giải chi tiết cho hàm số cụ thể, bao gồm các bước tính toán, phân tích và kết luận. Ví dụ:)
Để giúp học sinh hiểu rõ hơn về cách giải bài 1.23 trang 29, chúng ta sẽ xét một ví dụ cụ thể. (Ví dụ sẽ được trình bày chi tiết với các bước giải rõ ràng).
Để rèn luyện kỹ năng giải bài tập về hàm số và đồ thị, học sinh có thể làm thêm các bài tập tương tự sau:
Bài 1.23 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đồ thị. Bằng cách áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 1.23 trang 29 này sẽ giúp các em học sinh học tập hiệu quả và đạt được thành công trong môn Toán.