Bài 1.20 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật lời giải mới nhất và chính xác nhất, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB.
Đề bài
Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V(O, 2), V(I, – 2).
Phương pháp giải - Xem chi tiết
Tìm ảnh của điểm A, B qua phép vị tự V(O, 2), V(I, – 2) là A’, B’. Khi đó, ảnh của của đoạn thẳng AB là A’B’.
Lời giải chi tiết
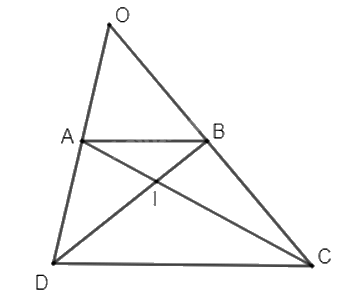
+ Vì ABCD là hình thang có hai đáy AB và CD nên AB // CD. Theo định lí Thales trong tam giác OCD ta có: \(\frac{{OA}}{{OD}} = \frac{{OB}}{{OC}} = \frac{{AB}}{{CD}} = \frac{1}{2}\).
Suy ra \(\overrightarrow {OD} = 2\overrightarrow {OA} ;\,\,\overrightarrow {OC} = 2\overrightarrow {OB} \).
Do đó, D và C tương ứng là ảnh của A và B qua phép vị tự \({V_{\left( {O,2} \right)}}\). Vậy đoạn thẳng DC là ảnh của đoạn thẳng AB qua phép vị tự \({V_{\left( {O,2} \right)}}\).
+ Vì AB // CD nên theo hệ quả của định lí Thales trong tam giác ICD ta có:
\(\frac{{IA}}{{IC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}} = \frac{1}{2}\)
Suy ra \(\overrightarrow {IC} = - 2\overrightarrow {IA} ;\,\,\overrightarrow {ID} = - 2\overrightarrow {IB} \).
Do đó, C và D tương ứng là ảnh của A và B qua phép vị tự \({V_{\left( {I,-2} \right)}}\). Vậy đoạn thẳng CD là ảnh của đoạn thẳng AB qua phép vị tự \({V_{\left( {I,-2} \right)}}\).
Bài 1.20 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến sự thay đổi của một đại lượng. Để giải bài này, chúng ta cần thực hiện các bước sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Một vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2. Tính vận tốc và gia tốc của vật tại thời điểm t = 2.)
Giải:
Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Để củng cố kiến thức, các em có thể tham khảo các bài tập tương tự sau:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em tự tin chinh phục môn Toán.
| Hàm số y = f(x) | Đạo hàm y' = f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |
Hy vọng với hướng dẫn chi tiết này, các em sẽ hiểu rõ cách giải bài 1.20 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức và tự tin giải các bài tập tương tự. Chúc các em học tốt!