Bài 3.9 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh phải tính đạo hàm, tìm cực trị và vẽ đồ thị hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
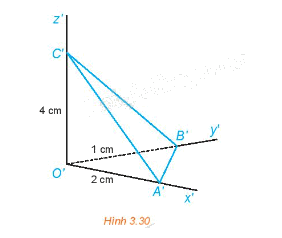
Cho hình tứ diện OABC có OA = 2 cm, OB = 3 cm và OC = 6 cm.
Đề bài
Cho hình tứ diện OABC có OA = 2 cm, OB = 3 cm và OC = 6 cm. Hình chiếu trục đo của hình tứ diện được cho như trong Hình 3.30. Tính hệ số biến dạng theo mỗi trục đo.
Phương pháp giải - Xem chi tiết
Các tỉ số \(p = \frac{{O'A'}}{{OA}},q = \frac{{O'B'}}{{OB}},r = \frac{{O'C'}}{{OC}}\) lần lượt là hệ số biến dạng theo trục \(O'x';\,\,O'y';\,\,O'z'\).
Lời giải chi tiết
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
\(\begin{array}{l}p = \frac{{O'A'}}{{OA}} = \frac{2}{2} = 1\\q = \frac{{O'B'}}{{OB}} = \frac{1}{3}\\r = \frac{{O'C'}}{{OC}} = \frac{4}{6} = \frac{2}{3}\end{array}\)
Bài 3.9 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến việc khảo sát hàm số bậc ba bằng phương pháp đạo hàm. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2. Ta sẽ thực hiện các bước như sau:
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Khi giải bài tập về khảo sát hàm số, cần chú ý các điểm sau:
Việc khảo sát hàm số có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng hướng dẫn chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về cách giải bài 3.9 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!