Bài 2.19 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:
Đề bài
Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:
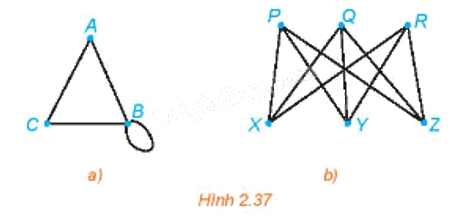
Phương pháp giải - Xem chi tiết
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết
a) Với đồ thị Hình 2.37 a) ta có:
+ Tập hợp các đỉnh là V(G) = {A; B; C};
+ Tập hợp các cạnh là E(G) = {AB; AC; BC; BB}.
b) Với đồ thị Hình 2.37 b) ta có:
+ Tập hợp các đỉnh là V(G) = {P; Q; R; X; Y; Z};
+ Tập hợp các cạnh là E(G) = {PX; PY; PZ; QX; QY; QZ; RX; RY; RZ}.
Bài 2.19 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm điểm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Để minh họa các bước trên, chúng ta hãy xem xét một ví dụ cụ thể. Giả sử hàm số được đề cập trong bài toán là f(x) = x^3 - 3x^2 + 2. Chúng ta sẽ thực hiện các bước sau:
Việc giải bài 2.19 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về đạo hàm mà còn có nhiều ứng dụng thực tế. Ví dụ, trong lĩnh vực kinh tế, đạo hàm được sử dụng để tìm điểm tối ưu hóa lợi nhuận hoặc chi phí. Trong lĩnh vực vật lý, đạo hàm được sử dụng để tính vận tốc và gia tốc của một vật thể. Do đó, việc hiểu rõ và vận dụng thành thạo kiến thức về đạo hàm là rất quan trọng đối với học sinh.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết và giải đáp thắc mắc.
Bài 2.19 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các bước giải và thực hành thường xuyên, bạn có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.