Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 3 trang 18, 19 của Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
Cho hình hình hành ABCD có hai đường chéo cắt nhau tại O. Tìm ảnh của đường thẳng AB qua \(Đ_{O}\)
Phương pháp giải:
- Tìm ảnh của từng điểm A, B qua . Sau đó nối chúng với nhau ta được ảnh của AB qua \(Đ_{O}\)
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \(Đ_{O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
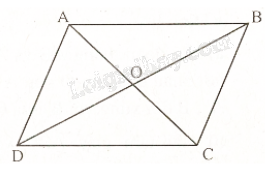
Vì ABCD là hình bình hành nên AC cắt BD tại O với O là trung điểm của AC và BD.
Do đó, C là ảnh của A qua phép đối xứng tâm O; D là ảnh của B qua phép đối xứng tâm O.
Vậy CD là ảnh của AB qua phép đối xứng tâm O.
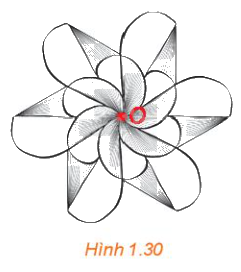
Quan sát Hình 1.30, những phát biểu nào trong các phát biểu sau là đúng?
a) Hình vẽ nhận điểm O (được tô đỏ) làm tâm đối xứng.
b) Một đường thẳng bất kì đi qua điểm O sẽ chia hình vẽ thành hai nửa A và B giống nhau. Nếu thực hiện phép quay tâm O, góc quay 180∘ thì nửa A biến thành nửa B, tức là, B là ảnh của A qua một phép đối xứng tâm O.
c) Có thể chia hình vẽ thành bốn phần giống nhau.
Phương pháp giải:
Quan sát hình 1.30 và dựa vào kiến thức: Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Phát biểu a, b, c đều đúng.
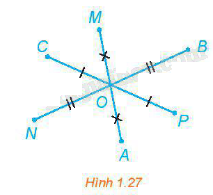
Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
Ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \) lần lượt là M, N, P, A, B, C.
Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
Ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \) lần lượt là M, N, P, A, B, C.
Cho hình hình hành ABCD có hai đường chéo cắt nhau tại O. Tìm ảnh của đường thẳng AB qua \(Đ_{O}\)
Phương pháp giải:
- Tìm ảnh của từng điểm A, B qua . Sau đó nối chúng với nhau ta được ảnh của AB qua \(Đ_{O}\)
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \(Đ_{O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
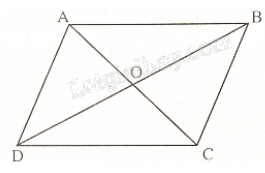
Vì ABCD là hình bình hành nên AC cắt BD tại O với O là trung điểm của AC và BD.
Do đó, C là ảnh của A qua phép đối xứng tâm O; D là ảnh của B qua phép đối xứng tâm O.
Vậy CD là ảnh của AB qua phép đối xứng tâm O.
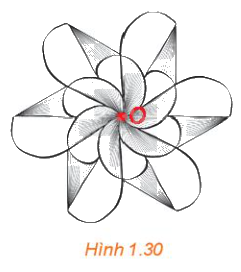
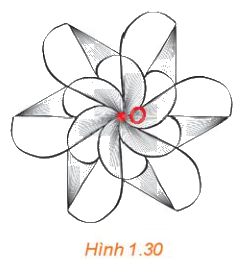
Quan sát Hình 1.30, những phát biểu nào trong các phát biểu sau là đúng?
a) Hình vẽ nhận điểm O (được tô đỏ) làm tâm đối xứng.
b) Một đường thẳng bất kì đi qua điểm O sẽ chia hình vẽ thành hai nửa A và B giống nhau. Nếu thực hiện phép quay tâm O, góc quay 180∘ thì nửa A biến thành nửa B, tức là, B là ảnh của A qua một phép đối xứng tâm O.
c) Có thể chia hình vẽ thành bốn phần giống nhau.
Phương pháp giải:
Quan sát hình 1.30 và dựa vào kiến thức: Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Phát biểu a, b, c đều đúng.
Mục 3 của Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào việc nghiên cứu về một chủ đề cụ thể trong chương trình Toán 11. Để hiểu rõ hơn về nội dung này, chúng ta cần xem xét các khái niệm, định lý và phương pháp giải bài tập liên quan. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách giải các bài tập trong mục 3 trang 18, 19, giúp bạn tự tin hơn trong quá trình học tập.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của mục 3. Mục này thường bao gồm các phần sau:
Lời giải:
Để giải bài tập này, chúng ta cần áp dụng (giải thích cách áp dụng kiến thức và công thức). Thực hiện các bước sau:
Kết quả cuối cùng là (kết quả).
Lời giải:
Tương tự như bài 1, chúng ta sẽ áp dụng (giải thích cách áp dụng kiến thức và công thức)....
Lời giải:
...
Lời giải:
...
Để giải các bài tập Toán 11 một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Kiến thức trong mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Hy vọng rằng bài viết này đã cung cấp cho bạn một hướng dẫn chi tiết về cách giải các bài tập trong mục 3 trang 18, 19 của Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc bạn học tập tốt và đạt kết quả cao!