Bài 2.16 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
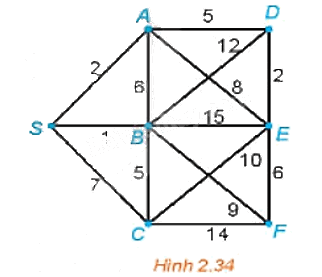
Tìm đường đi ngắn nhất từ đỉnh S đến mỗi đỉnh khác của đồ thị có trọng số trên Hình 2.34.
Đề bài
Tìm đường đi ngắn nhất từ đỉnh S đến mỗi đỉnh khác của đồ thị có trọng số trên Hình 2.34.
Phương pháp giải - Xem chi tiết
Giải bài tán bằng thuật toán tìm đường đi ngắn nhất: Ta xuất phát từ đỉnh A và di chuyển theo các cạnh của đồ thị. Với mỗi đỉnh V, ta gắn một số \(I(V)\) là khoảng cách ngắn nhất để đi từ A đến V, gọi là nhãn vĩnh viễn của đỉnh V. Như vậy, để tìm độ dài của đường đi ngắn nhất nối A với F, ta cần tìm \(I(F)\).
Lời giải chi tiết
Đầu tiên ta gắn nhãn đỉnh S là I(S) = 0 và gắn cho ba đỉnh kề với S là A, B và C các nhãn tạm thời là I(S) + 2, I(S) + 1 và I(S) + 7. Chọn số nhỏ nhất trong chúng và viết I(B) = 1. Đỉnh B bây giờ được gắn nhãn vĩnh viễn là 1.
Tiếp theo ta gắn nhãn cho các đỉnh kề với B là A, C, D, E và F các nhãn tạm thời là I(B) + 6 (hiện A có 2 nhãn tạm thời là 2 và 7), I(B) + 5 (hiện C có hai nhãn tạm thời là 7 và 6), I(B) + 12, I(B) + 15, I(B) + 9. Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (tại A, C, D, E, F) hiện nay là 2 (tại A), nên ta viết I(A) = 2. Điểm A được gắn nhãn vĩnh viễn là 2.
Bây giờ ta xét các đỉnh kề với A mà chưa được gắn nhãn vĩnh viễn là D và E. Ta gắn cho đỉnh D nhãn tạm thời I(A) + 5 (hiện D có hai nhãn tạm thời là 13 và 7), gắn cho đỉnh E nhãn tạm thời I(A) + 8 (hiện E có hai nhãn tạm thời là 16 và 10). Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (tại D và E) là 7 (tại D), nên ta viết I(D) = 7. Đỉnh D được gắn nhãn vĩnh viễn là 7.
Ta xét đỉnh E (chưa được gắn nhãn vĩnh viễn) kề với D, ta gắn nhãn tạm thời I(D) + 2 (hiện E có ba nhãn tạm thời là 16, 10 và 9). Vậy đỉnh E sẽ được gắn nhãn vĩnh viễn là 9 hay I(E) = 9.
Tiếp tục ta xét các đỉnh kề với E mà chưa được gắn nhãn vĩnh viễn là C và F. Ta gắn cho đỉnh C nhãn tạm thời I(E) + 10 (hiện C có ba nhãn tạm thời là 7, 6 và 19), gắn cho F nhãn tạm thời I(E) + 6 (hiện F có hai nhãn tạm thời là 10 và 15). Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (ở C, F) hiện nay là 6 (tại C), nên ta viết I(C) = 6. Đỉnh C được gắn nhãn vĩnh viễn là 6.
Xét đỉnh kề với C là F, ta gắn cho F nhãn tạm thời I(C) + 14 (hiện F có ba nhãn tạm thời là 10, 15 và 20) nên I(F) = 10. Đỉnh F được gắn nhãn vĩnh viễn là 10.
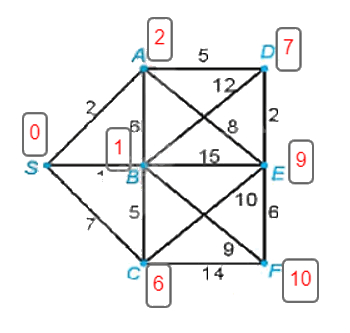
Vậy, đường đi ngắn nhất từ đỉnh S đến đỉnh A là SA = 2.
Đường đi ngắn nhất từ đỉnh S đến đỉnh B là SB = 1.
Đường đi ngắn nhất từ đỉnh S đến đỉnh C có độ dài là I(C) = 6 và có đường đi là
S → B → C.
Đường đi ngắn nhất từ đỉnh S đến đỉnh D có độ dài là I(D) = 7 và đường đi là
S → A → D.
Đường đi ngắn nhất từ đỉnh S đến đỉnh E có độ dài là I(E) = 9 và đường đi là
S → A → D → E.
Đường đi ngắn nhất từ đỉnh S đến đỉnh F có độ dài là I(F) = 10 và đường đi là
S → B → F.
Bài 2.16 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm điểm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Để minh họa các bước trên, chúng ta sẽ cùng nhau giải bài 2.16 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức. (Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước tính toán, phân tích và kết luận cụ thể. Ví dụ:)
Ví dụ: Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
Việc giải bài 2.16 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về đạo hàm mà còn có nhiều ứng dụng thực tế:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Hãy nhớ áp dụng các bước giải đã học và kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài 2.16 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các bước giải và luyện tập thường xuyên, bạn sẽ tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.