Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập mở đầu trang 41 Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúng tôi hiểu rằng việc giải các bài tập này có thể gặp nhiều khó khăn, đặc biệt là với những học sinh mới làm quen với chương trình.
Bài viết này sẽ cung cấp cho bạn đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn có thể tự tin giải quyết các bài toán tương tự.
Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga)
Đề bài
Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?
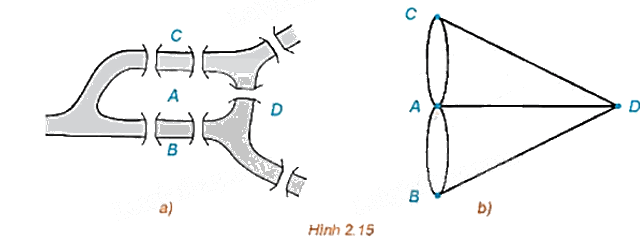
Nếu ta coi mỗi khu vực A, B, C, D của thành phố là một đỉnh, mỗi cầu qua lại hai khu vực như một cạnh nối hai đỉnh, thì bản đồ thành phố Königsberg là một đa đồ thị như Hình 2.15b. Vấn đề đặt ra chính là: Có thể vẽ được Hình 2.15b bằng một nét liền hay không?
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ và suy luận thực tế để trả lời
Lời giải chi tiết
Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:
Xét đa đồ thị G ở Hình 2.15b. Vì các đỉnh A, B, C, D đều có bậc lẻ nên theo Định lí 2, G không có đường đi Euler và không có cả chu trình Euler.
Vậy không thể nào đi dạo qua khắp các cây cầu của thành phố Königsberg mà mỗi cầu chỉ đi qua một lần.
Bài tập mở đầu trang 41 trong Chuyên đề học tập Toán 11 - Kết nối tri thức đóng vai trò quan trọng trong việc giúp học sinh làm quen với các khái niệm và kỹ năng mới được giới thiệu trong chương. Bài tập này thường mang tính chất tổng hợp, đòi hỏi học sinh phải vận dụng kiến thức đã học từ các chương trước để giải quyết vấn đề.
Bài tập mở đầu trang 41 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường kiểm tra khả năng hiểu khái niệm và nhận biết các yếu tố liên quan đến bài học. Bài tập tự luận yêu cầu học sinh phải trình bày lời giải chi tiết, chứng minh các kết luận và áp dụng các công thức đã học.
Để giải bài tập mở đầu trang 41 hiệu quả, học sinh cần:
Bài tập: (Giả sử một bài tập cụ thể từ trang 41 được đưa ra ở đây).
Lời giải: (Giải chi tiết bài tập, bao gồm các bước giải, công thức sử dụng và kết luận).
Để đạt kết quả tốt nhất khi giải bài tập mở đầu trang 41, học sinh cần:
Việc giải bài tập mở đầu trang 41 không chỉ giúp học sinh củng cố kiến thức đã học mà còn giúp học sinh phát triển tư duy logic, khả năng giải quyết vấn đề và kỹ năng tự học. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong các môn học khác và trong cuộc sống.
Bài tập mở đầu trang 41 Chuyên đề học tập Toán 11 - Kết nối tri thức là một phần quan trọng trong quá trình học tập môn Toán. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và áp dụng các phương pháp giải hiệu quả, học sinh có thể tự tin giải quyết các bài tập này và đạt kết quả tốt nhất.