Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!

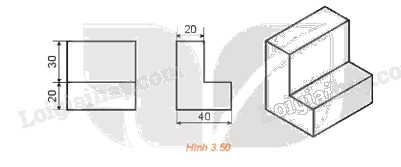
Bản vẽ trong Hình 3.50 có đáp ứng các nguyên tắc cơ bản của vẽ kĩ thuật hay không? Giải thích vì sao.

Đề bài

Bản vẽ trong Hình 3.50 có đáp ứng các nguyên tắc cơ bản của vẽ kĩ thuật hay không? Giải thích vì sao.

Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Bản vẽ kĩ thuật cẩn đảm bảo các nguyên tắc cơ bản sau:

- Nguyên tắc phản chuyển: các hình biểu diễn trên bản vẽ kĩ thuật xác định duy nhất hình dạng và cấu tạo của vật thể được biểu diễn.

- Nguyên tắc đầy đủ: Các kích thước của vật thể được biểu diễn đầy đủ trên bản vẽ kĩ thuật.

Lời giải chi tiết

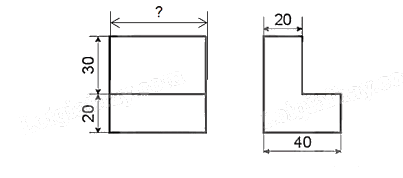
Bản vẽ trong Hình 3.50 thể hiện duy nhất một vật thể cần được biểu diễn, tuy nhiên kích thước của vật thể không được xác định đầy đủ từ bản vẽ nên bản vẽ không đáp ứng được nguyên tắc đầy đủ của vẽ kĩ thuật. Kích thước bị thiếu là:

Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức 3

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng toán math. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần nắm vững các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm bậc nhất: Sử dụng các quy tắc đạo hàm để tìm đạo hàm f'(x).
Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
Lập bảng biến thiên: Xác định dấu của đạo hàm f'(x) trên các khoảng xác định để xác định khoảng hàm số đồng biến, nghịch biến.
Kết luận về cực trị: Dựa vào bảng biến thiên để xác định các điểm cực đại, cực tiểu của hàm số.

Lời giải chi tiết bài 3.18 trang 80

Đề bài: (Giả sử đề bài cụ thể của bài 3.18 được đưa ra ở đây. Ví dụ: Tìm cực đại, cực tiểu của hàm số y = x^3 - 3x^2 + 2)

Giải:

Tập xác định: Hàm số y = x^3 - 3x^2 + 2 có tập xác định là D = ℝ.
Đạo hàm bậc nhất: y' = 3x^2 - 6x.
Điểm dừng: Giải phương trình 3x^2 - 6x = 0, ta được x = 0 hoặc x = 2.
Bảng biến thiên:
x -∞ 0 2 +∞
y' + - +
y ↗ ↘ ↗
Kết luận: Hàm số đạt cực đại tại x = 0, y = 2 và đạt cực tiểu tại x = 2, y = -2.

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

Lưu ý khi giải bài tập về cực trị

Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
Chú ý các trường hợp đạo hàm không tồn tại tại một điểm nào đó.
Sử dụng bảng biến thiên để xác định chính xác khoảng hàm số đồng biến, nghịch biến và các điểm cực trị.
Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.

Ứng dụng của việc tìm cực trị

Việc tìm cực trị của hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:

Trong kinh tế: Tìm điểm tối ưu để đạt lợi nhuận cao nhất hoặc chi phí thấp nhất.
Trong kỹ thuật: Tìm điểm ổn định của hệ thống.
Trong vật lý: Tìm điểm cân bằng của vật thể.

Tổng kết

Bài 3.18 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về khái niệm cực trị của hàm số và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết này, các bạn học sinh có thể tự tin giải bài tập và nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm.