Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 1 trang 41, 42 của Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
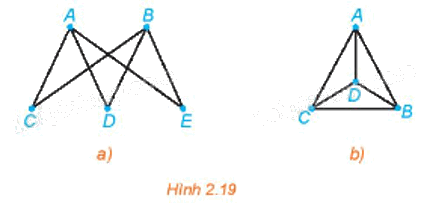
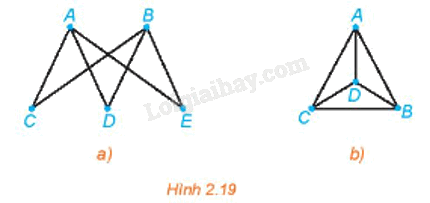
- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.
- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
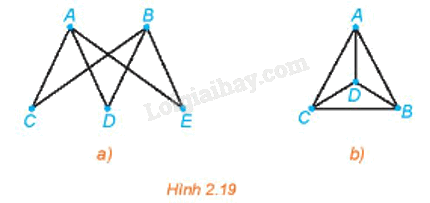
- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.
- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
Phương pháp giải:
Quan sát hình 2.16 để làm
Lời giải chi tiết:
Ta có thể vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
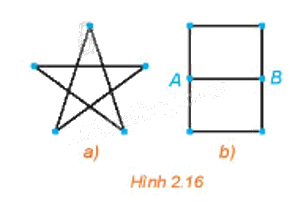
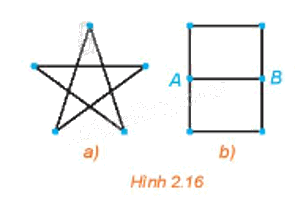
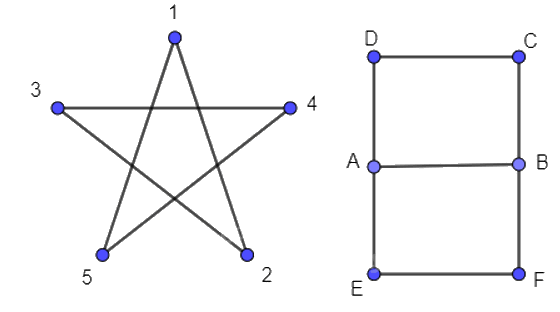
- Đối với Hình 2.16 a), ta có thể vẽ một nét liền theo thứ tự 123451.
- Đối với Hình 2.16 b), ta có thể vẽ một nét liền theo thứ tự ABCDAEFB.
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
Phương pháp giải:
Quan sát hình 2.16 để làm
Lời giải chi tiết:
Ta có thể vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
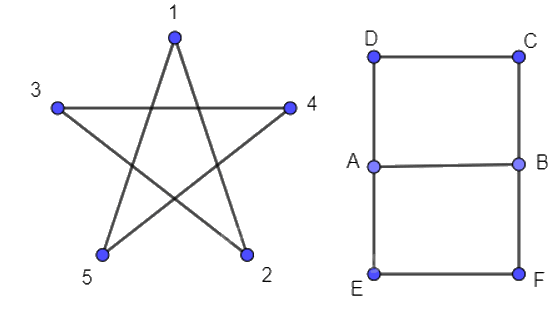
- Đối với Hình 2.16 a), ta có thể vẽ một nét liền theo thứ tự 123451.
- Đối với Hình 2.16 b), ta có thể vẽ một nét liền theo thứ tự ABCDAEFB.
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.
- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
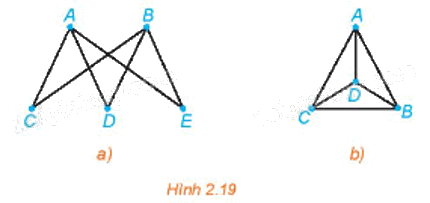
- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.
- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc hai. Các bài tập trong trang 41 và 42 thường xoay quanh việc xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Bài tập này yêu cầu học sinh xác định chính xác các hệ số a, b, c trong hàm số bậc hai có dạng y = ax2 + bx + c. Việc này đòi hỏi học sinh phải nắm vững định nghĩa và cách nhận biết các hệ số trong hàm số.
Để tìm đỉnh của parabol, học sinh cần sử dụng công thức xđỉnh = -b/2a và yđỉnh = f(xđỉnh). Đỉnh của parabol là điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) trên đồ thị hàm số.
Để vẽ đồ thị hàm số bậc hai, học sinh cần xác định các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với trục Oy và một vài điểm khác trên đồ thị. Sau đó, vẽ parabol đi qua các điểm đã xác định.
Các bài toán ứng dụng hàm số bậc hai thường liên quan đến việc tìm giá trị lớn nhất hoặc nhỏ nhất của một đại lượng nào đó, hoặc giải các bài toán về quỹ đạo chuyển động của vật thể.
Ví dụ: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy tìm độ cao lớn nhất mà quả bóng đạt được. (Giả sử gia tốc trọng trường là g = 9.8 m/s2).
Lời giải: Độ cao của quả bóng được mô tả bởi hàm số h(t) = 15t - 4.9t2. Để tìm độ cao lớn nhất, ta cần tìm đỉnh của parabol. xđỉnh = -15/(2*(-4.9)) ≈ 1.53. h(1.53) ≈ 11.48. Vậy độ cao lớn nhất mà quả bóng đạt được là khoảng 11.48 mét.
Việc giải các bài tập trong mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức đòi hỏi học sinh phải nắm vững kiến thức cơ bản về hàm số bậc hai và rèn luyện kỹ năng giải toán thường xuyên. Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn khi đối mặt với các bài tập toán học.