Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải quyết bài tập mở đầu trang 68 trong Chuyên đề học tập Toán 11 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
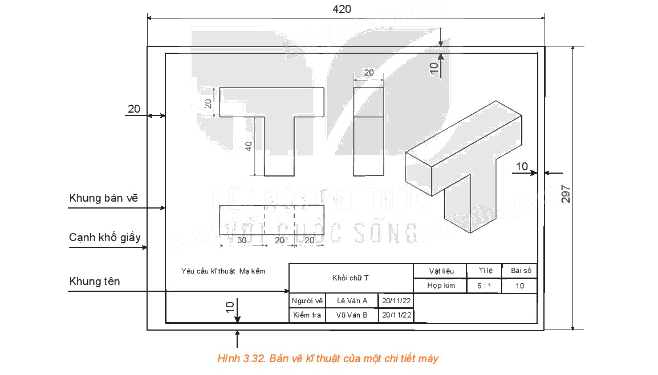
Bản vẽ kĩ thuật của một vật thể là tài liệu mô tả chính xác hình dạng, kết cấu và kích thước của vật thể đó.
Đề bài
Bản vẽ kĩ thuật của một vật thể là tài liệu mô tả chính xác hình dạng, kết cấu và kích thước của vật thể đó. Bản vẽ kĩ thuật cần tuân thủ các nguyên tắc nào? Làm thế nào để đọc được thông tin từ một bản vẽ kĩ thuật và lập một bản vẽ kĩ thuật đơn giản?
Phương pháp giải - Xem chi tiết
Quan sát hình 3.32 để làm
Lời giải chi tiết
- Bản vẽ kĩ thuật cần tuân thủ các nguyên tắc:
+ Nguyên tắc phản chuyển: các hình biểu diễn trên bản vẽ kĩ thuật xác định duy nhất hình dạng và cấu tạo của vật thể được biểu diễn.
+ Nguyên tắc đầy đủ: các kích thước của vật thể được biểu diễn đầy đủ trên bản vẽ kĩ thuật.
- Đọc thông tin từ bản vẽ kĩ thuật cần tuân theo trình tự sau:
+ Khung tên: xác định tên gọi của vật thể, vật liệu sử dụng để chế tạo vật thể, tỉ lệ bản vẽ.
+ Hình biểu diễn: xác định tên gọi của các hình chiếu có trong bản vẽ và các hình biểu diễn khác (nếu có).
+ Kích thước: xác định kích thước chung của vật thể và kích thước các thành phần.
+ Yêu cầu kĩ thuật: xác định yêu cầu về gia công, xử lí bề mặt của vật thể.
- Lập bản vẽ kĩ thuật của một vật thể ta thực hiện theo các bước sau:
+ Bước 1: Quan sát vật thể và phân tích vật thể thành các hình khối đơn giản.
+ Bước 2: Chọn các hướng chiếu phù hợp, thường là các hướng vuông góc với các mặt của vật thể.
+ Bước 3: Vẽ hình chiếu vuông góc của các hình khối cấu tạo nên vật thể.
+ Bước 4: Xóa các nét thừa, chỉnh sửa các nét vẽ theo đúng tiêu chuẩn và ghi kích thước trên các hình chiếu.
+ Bước 5: Từ ba hình chiếu vuông góc vừa vẽ, vẽ hình chiếu trục đo vuông góc đều của vật thể.
+ Bước 6: Kẻ khung bản vẽ, khung tên, ghi các nội dung vào khung tên để hoàn thành bản vẽ.
Bài tập mở đầu trang 68 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường đóng vai trò quan trọng trong việc đặt nền móng cho các kiến thức tiếp theo. Nó không chỉ kiểm tra sự hiểu biết của học sinh về các khái niệm cơ bản mà còn rèn luyện kỹ năng vận dụng kiến thức vào giải quyết các vấn đề thực tế. Do đó, việc nắm vững phương pháp giải bài tập này là vô cùng cần thiết.
Bài tập mở đầu trang 68 thường xoay quanh các chủ đề chính của chương, ví dụ như:
Để giải quyết hiệu quả bài tập mở đầu trang 68, bạn có thể áp dụng các phương pháp sau:
Bài tập: Giải phương trình lượng giác sau: sin(x) = 1/2
Giải:
Phương trình sin(x) = 1/2 có nghiệm là:
Khi giải bài tập mở đầu trang 68, bạn cần lưu ý những điều sau:
Để hỗ trợ quá trình học tập và giải bài tập, bạn có thể tham khảo các tài liệu sau:
Bài tập mở đầu trang 68 trong Chuyên đề học tập Toán 11 - Kết nối tri thức là một phần quan trọng trong quá trình học tập môn Toán. Bằng cách nắm vững phương pháp giải bài tập và rèn luyện kỹ năng thường xuyên, bạn có thể tự tin đối mặt với các bài toán khó và đạt kết quả tốt trong môn học này. Chúc bạn học tập tốt!
| Chủ đề | Phương pháp |
|---|---|
| Hàm số lượng giác | Xác định tập xác định, tập giá trị, tính đơn điệu, cực trị |
| Phương trình lượng giác | Biến đổi lượng giác, sử dụng công thức nghiệm |
| Đạo hàm lượng giác | Tính đạo hàm, ứng dụng đạo hàm |