Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 56, 57, 58, 59 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh muốn học toán online hiệu quả. Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải, đáp án các bài tập trong sách giáo khoa và các chuyên đề học tập.
Trong không gian cho điểm A và hai mặt phẳng hình chiếu đứng, hình chiếu bằng (P1), (P2)
Dựa vào mối liên hệ giữa ba hình chiếu, giải thích cách bố trí các hình chiếu trên bản vẽ kĩ thuật. Vì sao đối với một số vật thể đơn giản, bản vẽ kĩ thuật chỉ thể hiện hai thay vì ba hình chiếu?
Phương pháp giải:
Dựa vào kiến thức đã học để trả lời
Lời giải chi tiết:
Đối với một số vật thể đơn giản, bản vẽ kĩ thuật chỉ thể hiện hai thay vì ba hình chiếu vì từ hai hình chiếu cho trước ta có thể xác định được hình chiếu các đoạn thẳng thuộc hình chiếu còn lại từ hình chiếu các đoạn thẳng ở hai hình chiếu cho trước.
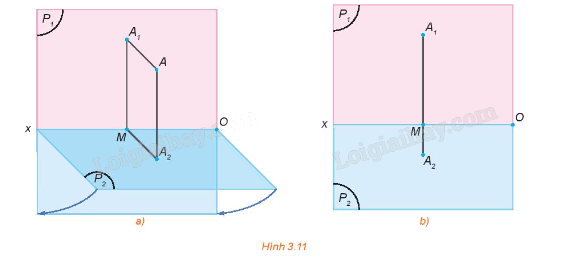
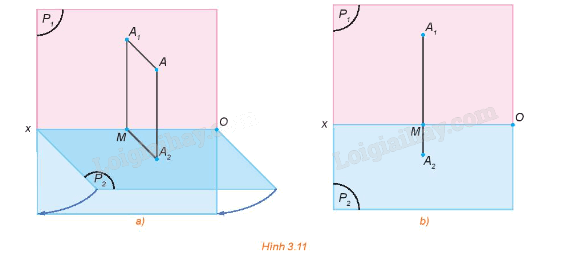
Trong không gian cho điểm A và hai mặt phẳng hình chiếu đứng, hình chiếu bằng (P1), (P2) cắt nhau theo giao tuyến Ox. Gọi A1 và A2 lần lượt là hình chiếu đứng và hình chiếu bằng của điểm A (H.3.11a). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1). Khi đó hai điểm A1 và A2 cùng thuộc mặt phẳng (P1) (H.3.11b).
a) Nhận xét vị trí của các điểm A1, A2 đối với đường thẳng Ox. Đường thẳng A1A2 có vuông góc với Ox hay không?
b) Hãy trình bày cách xác định điểm A khi biết các điểm A1, A2 trong mặt phẳng (P1).
Phương pháp giải:
Quan sát hình 3.11 để trả lời
Lời giải chi tiết:
a) Điểm A1 và điểm A2 nằm về hai phía khác nhau đối với đường thẳng Ox. Đường thẳng A1A2 có vuông góc với Ox.
b) Ta có: A1M = AA2 (do tứ giác A1MA2A là hình chữ nhật).
Từ A2 kẻ đường thẳng A2A bằng đường thẳng A1M (A thuộc A1A2). Ta xác định được điểm A.
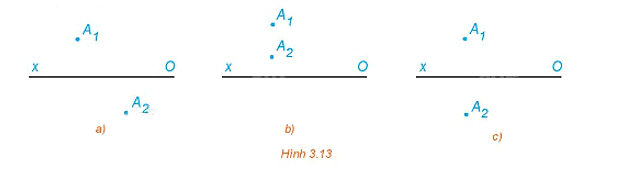
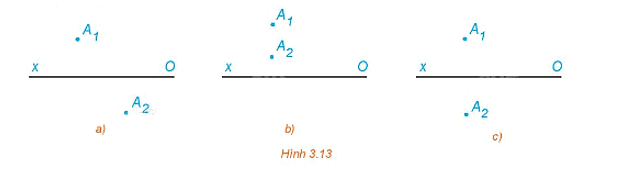
Trong Hình 3.13, hình nào thể hiện đúng hình chiếu đứng và hình chiếu bằng của một điểm A trong không gian?
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
Nếu A1 và A2 là hình chiếu đứng và hình chiếu bằng của điểm A thì đường thẳng A1A2 vuông góc với Ox. Do đó Hình 3.13c thể hiện đúng hai hình chiếu của điểm A.
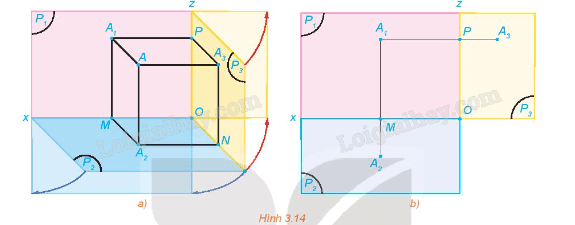
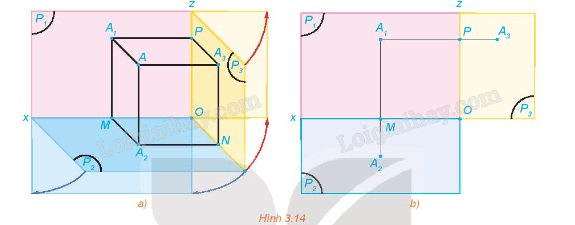
Trong HĐ2, gọi (P3) là mặt phẳng hình chiếu cạnh và A3 là hình chiếu cạnh của A. Gọi Oz là giao tuyến của (P1) và (P3), Oy là giao tuyến của (P2) và (P3). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1) và quay mặt phẳng (P3) quanh Oz sao cho (P3) trùng với (P1), khi đó ba điểm A1, A2, A3 cùng thuộc mặt phẳng (P1) (H.3.14).
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz hay không? Khoảng cách từ A3 đến Oz có bằng khoảng cách từ A2 đến Ox hay không?
b) Trong mặt phẳng (P1), trình bày cách xác định điểm A3 khi biết hai điểm A1, A2.
Phương pháp giải:
Quan sát hình 3.14 để trả lời
Lời giải chi tiết:
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz. Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox.
b) Ta có A1A2 vuông góc với Ox nên gọi giao điểm của A1A2 với Ox là M.
Từ A1 kẻ đường thẳng song song với Ox và vuông góc với Oz. Gọi giao điểm của đường thẳng kẻ từ A1 với Oz là P.
Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox hay A2M = A3P. Từ P kẻ A3P sao cho A1, P, A3 thẳng hàng theo thứ tự và A2M = A3P.
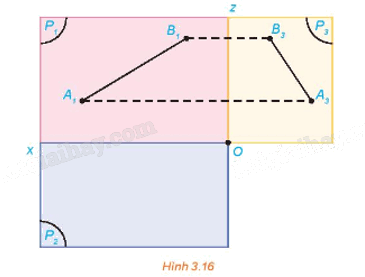
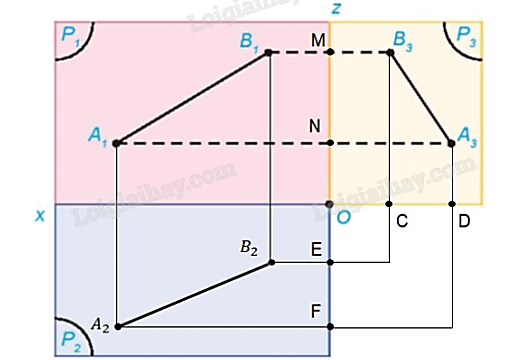
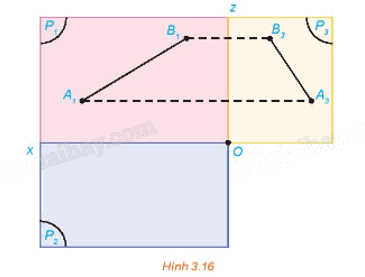
Hình 3.16 thể hiện hình chiếu đứng và hình chiếu cạnh của một đoạn thẳng AB trong không gian. Xác định hình chiếu bằng của đoạn thẳng đó
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
Hình chiếu bằng của đoạn thẳng AB có hai đầu mút là hình chiếu bằng A2 của A và hình chiếu bằng B2 của B.
+ Để xác định A2 ta làm như sau:
- Qua điểm A3 vẽ đường thẳng vuông góc với Ox tại D và trên tia đối của tia Oz lấy điểm F sao cho OD = OF.
- Vẽ đường thẳng qua A1 vuông góc với Ox, vẽ đường thẳng qua F vuông góc với Oz, hai đường thẳng này cắt nhau tại A2.
+ Tương tự xác định B2.
+ Nối A2 và B2 ta nhận được hình chiếu bằng của đoạn thẳng AB.
Trong không gian cho điểm A và hai mặt phẳng hình chiếu đứng, hình chiếu bằng (P1), (P2) cắt nhau theo giao tuyến Ox. Gọi A1 và A2 lần lượt là hình chiếu đứng và hình chiếu bằng của điểm A (H.3.11a). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1). Khi đó hai điểm A1 và A2 cùng thuộc mặt phẳng (P1) (H.3.11b).
a) Nhận xét vị trí của các điểm A1, A2 đối với đường thẳng Ox. Đường thẳng A1A2 có vuông góc với Ox hay không?
b) Hãy trình bày cách xác định điểm A khi biết các điểm A1, A2 trong mặt phẳng (P1).
Phương pháp giải:
Quan sát hình 3.11 để trả lời
Lời giải chi tiết:
a) Điểm A1 và điểm A2 nằm về hai phía khác nhau đối với đường thẳng Ox. Đường thẳng A1A2 có vuông góc với Ox.
b) Ta có: A1M = AA2 (do tứ giác A1MA2A là hình chữ nhật).
Từ A2 kẻ đường thẳng A2A bằng đường thẳng A1M (A thuộc A1A2). Ta xác định được điểm A.
Trong Hình 3.13, hình nào thể hiện đúng hình chiếu đứng và hình chiếu bằng của một điểm A trong không gian?
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
Nếu A1 và A2 là hình chiếu đứng và hình chiếu bằng của điểm A thì đường thẳng A1A2 vuông góc với Ox. Do đó Hình 3.13c thể hiện đúng hai hình chiếu của điểm A.
Trong HĐ2, gọi (P3) là mặt phẳng hình chiếu cạnh và A3 là hình chiếu cạnh của A. Gọi Oz là giao tuyến của (P1) và (P3), Oy là giao tuyến của (P2) và (P3). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1) và quay mặt phẳng (P3) quanh Oz sao cho (P3) trùng với (P1), khi đó ba điểm A1, A2, A3 cùng thuộc mặt phẳng (P1) (H.3.14).
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz hay không? Khoảng cách từ A3 đến Oz có bằng khoảng cách từ A2 đến Ox hay không?
b) Trong mặt phẳng (P1), trình bày cách xác định điểm A3 khi biết hai điểm A1, A2.
Phương pháp giải:
Quan sát hình 3.14 để trả lời
Lời giải chi tiết:
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz. Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox.
b) Ta có A1A2 vuông góc với Ox nên gọi giao điểm của A1A2 với Ox là M.
Từ A1 kẻ đường thẳng song song với Ox và vuông góc với Oz. Gọi giao điểm của đường thẳng kẻ từ A1 với Oz là P.
Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox hay A2M = A3P. Từ P kẻ A3P sao cho A1, P, A3 thẳng hàng theo thứ tự và A2M = A3P.
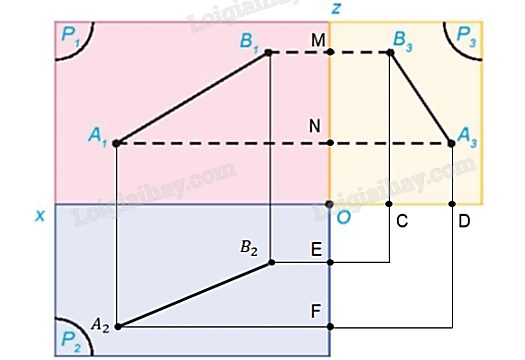
Hình 3.16 thể hiện hình chiếu đứng và hình chiếu cạnh của một đoạn thẳng AB trong không gian. Xác định hình chiếu bằng của đoạn thẳng đó
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
Hình chiếu bằng của đoạn thẳng AB có hai đầu mút là hình chiếu bằng A2 của A và hình chiếu bằng B2 của B.
+ Để xác định A2 ta làm như sau:
- Qua điểm A3 vẽ đường thẳng vuông góc với Ox tại D và trên tia đối của tia Oz lấy điểm F sao cho OD = OF.
- Vẽ đường thẳng qua A1 vuông góc với Ox, vẽ đường thẳng qua F vuông góc với Oz, hai đường thẳng này cắt nhau tại A2.
+ Tương tự xác định B2.
+ Nối A2 và B2 ta nhận được hình chiếu bằng của đoạn thẳng AB.
Dựa vào mối liên hệ giữa ba hình chiếu, giải thích cách bố trí các hình chiếu trên bản vẽ kĩ thuật. Vì sao đối với một số vật thể đơn giản, bản vẽ kĩ thuật chỉ thể hiện hai thay vì ba hình chiếu?
Phương pháp giải:
Dựa vào kiến thức đã học để trả lời
Lời giải chi tiết:
Đối với một số vật thể đơn giản, bản vẽ kĩ thuật chỉ thể hiện hai thay vì ba hình chiếu vì từ hai hình chiếu cho trước ta có thể xác định được hình chiếu các đoạn thẳng thuộc hình chiếu còn lại từ hình chiếu các đoạn thẳng ở hai hình chiếu cho trước.
Mục 3 trong Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào các kiến thức về đạo hàm của hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng áp dụng chúng vào giải bài tập.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số lý thuyết trọng tâm:
Ngoài ra, cần nhớ các quy tắc đạo hàm như quy tắc đạo hàm của tổng, hiệu, tích, thương và quy tắc đạo hàm hàm hợp.
Bài 1 (Trang 56): Tính đạo hàm của các hàm số sau:
Giải:
Bài 2 (Trang 57): Cho hàm số y = sin2 x. Tính y'.
Giải:
Áp dụng quy tắc đạo hàm hàm hợp: y' = 2sin x * cos x = sin 2x
Bài 3 (Trang 58): Tìm đạo hàm của hàm số y = cos(2x + 1).
Giải:
Áp dụng quy tắc đạo hàm hàm hợp: y' = -sin(2x + 1) * 2 = -2sin(2x + 1)
Bài 4 (Trang 59): Tính đạo hàm của hàm số y = tan3 x.
Giải:
Áp dụng quy tắc đạo hàm hàm hợp: y' = 3tan2 x * (1/cos2 x) = 3tan2 x / cos2 x
Để hiểu sâu hơn về đạo hàm của hàm số lượng giác, các em có thể tham khảo thêm các bài tập sau:
Khi giải các bài tập về đạo hàm của hàm số lượng giác, các em cần lưu ý:
Hy vọng bài giải chi tiết này sẽ giúp các em học tốt môn Toán 11. Chúc các em thành công!