Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 16, 17 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Chúng tôi cung cấp các bước giải bài tập rõ ràng, kèm theo giải thích chi tiết để các em có thể tự học và hiểu sâu sắc vấn đề.
Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới
Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới, thì mỗi đĩa không đặt ở chính giữa bàn có được quay một phần tư vòng tới vị trí mới hay không?
Phương pháp giải:
Suy luận thực tiễn để trả lời
Lời giải chi tiết:
Mỗi đĩa thức ăn không đặt ở chính giữa bàn nhưng đặt ở trên phần bàn xoay đều quay được một phần tư vòng tới vị trí mới.
Mỗi đĩa thức ăn không đặt ở giữa bàn và không đặt ở trên phần bàn xoay thì không quay được một phần tư vòng tới vị trí mới.
Phép quay với góc quay bằng 0 có gì đặc biệt?
Phương pháp giải:
Dựa vào phép quay \({Q_{\left( {O,\alpha } \right)}}\) với \(\alpha = {0^o}\).
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Phép quay tâm O với góc quay bằng 0 biến điểm O thành điểm O và biến mỗi điểm M khác O thành chính nó.
Trong Hình 1.22, tam giác ABC đều.
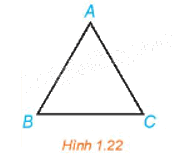
Hãy chỉ ra ảnh của điểm B qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\)
Gọi D là ảnh của C qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\)
Hỏi B và D có mối quan hệ gì đối với đường thẳng AC?
Phương pháp giải:
- Tam giác đều có 3 góc bằng \({60^o}\).
- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Tam giác ABC đều nên AB = AC và \(\widehat {BAC} = 60^\circ \). Do đó phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\) biến điểm B thành điểm C.
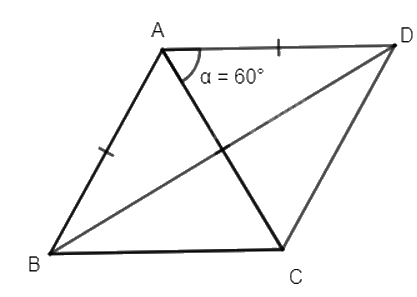
Vì D là ảnh của C qua phép quay Q(A, 60°) nên AC = AD và \(\widehat {CAD} = 60^\circ \)
Khi đó tam giác ACD là tam giác đều nên AC = AD = DC.
Mà AB = AC = BC (tam giác ABC đều).
Do đó, AB = BC = CD = AD, suy ra tứ giác ABCD là hình thoi.
Khi đó hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên AC là đường trung trực của đoạn thẳng BD.
Vậy B và D đối xứng nhau qua đường thẳng AC hay B là ảnh của D qua phép đối xứng trục AC.
Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới, thì mỗi đĩa không đặt ở chính giữa bàn có được quay một phần tư vòng tới vị trí mới hay không?
Phương pháp giải:
Suy luận thực tiễn để trả lời
Lời giải chi tiết:
Mỗi đĩa thức ăn không đặt ở chính giữa bàn nhưng đặt ở trên phần bàn xoay đều quay được một phần tư vòng tới vị trí mới.
Mỗi đĩa thức ăn không đặt ở giữa bàn và không đặt ở trên phần bàn xoay thì không quay được một phần tư vòng tới vị trí mới.
Phép quay với góc quay bằng 0 có gì đặc biệt?
Phương pháp giải:
Dựa vào phép quay \({Q_{\left( {O,\alpha } \right)}}\) với \(\alpha = {0^o}\).
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Phép quay tâm O với góc quay bằng 0 biến điểm O thành điểm O và biến mỗi điểm M khác O thành chính nó.
Trong Hình 1.22, tam giác ABC đều.
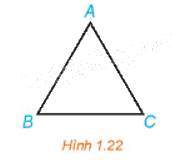
Hãy chỉ ra ảnh của điểm B qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\)
Gọi D là ảnh của C qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\)
Hỏi B và D có mối quan hệ gì đối với đường thẳng AC?
Phương pháp giải:
- Tam giác đều có 3 góc bằng \({60^o}\).
- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Tam giác ABC đều nên AB = AC và \(\widehat {BAC} = 60^\circ \). Do đó phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\) biến điểm B thành điểm C.
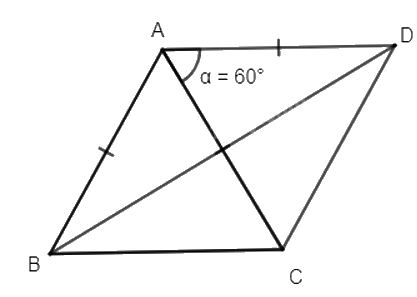
Vì D là ảnh của C qua phép quay Q(A, 60°) nên AC = AD và \(\widehat {CAD} = 60^\circ \)
Khi đó tam giác ACD là tam giác đều nên AC = AD = DC.
Mà AB = AC = BC (tam giác ABC đều).
Do đó, AB = BC = CD = AD, suy ra tứ giác ABCD là hình thoi.
Khi đó hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên AC là đường trung trực của đoạn thẳng BD.
Vậy B và D đối xứng nhau qua đường thẳng AC hay B là ảnh của D qua phép đối xứng trục AC.
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một khái niệm hoặc kỹ năng quan trọng trong chương trình. Việc nắm vững nội dung này là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ đi sâu vào phân tích từng bài tập trong mục 1 trang 16, 17, cung cấp lời giải chi tiết và các lưu ý quan trọng.
Bài tập này yêu cầu chúng ta… (Mô tả yêu cầu bài tập). Để giải bài tập này, chúng ta cần áp dụng kiến thức về… (Liệt kê các kiến thức liên quan). Các bước giải như sau:
Kết quả cuối cùng là… (Kết quả bài tập).
Bài tập này liên quan đến… (Mô tả yêu cầu bài tập). Để giải quyết bài toán này, chúng ta cần sử dụng công thức… (Liệt kê các công thức liên quan). Cách giải:
Vậy đáp án của bài tập là… (Kết quả bài tập).
Bài tập này đòi hỏi chúng ta phải kết hợp kiến thức về… (Liệt kê các kiến thức liên quan). Chúng ta sẽ giải bài tập này bằng phương pháp…
| Bước | Thực hiện | Giải thích |
|---|---|---|
| 1 | … | … |
| 2 | … | … |
| 3 | … | … |
| Kết quả cuối cùng: … (Kết quả bài tập) | ||
Khi giải các bài tập trong mục 1 trang 16, 17 Chuyên đề học tập Toán 11 - Kết nối tri thức, các em cần lưu ý những điều sau:
Kiến thức và kỹ năng được học trong mục 1 trang 16, 17 Chuyên đề học tập Toán 11 - Kết nối tri thức có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của Toán học, đặc biệt là trong các chương tiếp theo của môn Toán 11. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán phức tạp hơn một cách dễ dàng và hiệu quả.
Hy vọng rằng bài viết này đã cung cấp cho các em những lời giải chi tiết và dễ hiểu cho mục 1 trang 16, 17 Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!