Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Kết nối tri thức. Chúng tôi tập trung vào việc giúp học sinh nắm vững kiến thức và kỹ năng giải toán một cách hiệu quả.
Mục 4 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường chứa các bài tập về một chủ đề cụ thể. Chúng tôi sẽ cung cấp các bước giải chi tiết, rõ ràng, kèm theo giải thích để bạn hiểu rõ bản chất của bài toán.
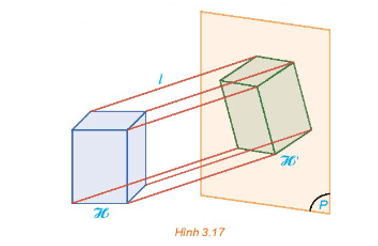
Cho hình hộp chữ nhật ℋ. Quan sát hình chiếu song song ℋ ' của hình ℋ lên mặt phẳng (P) theo phương l (H.3.17) và trả lời các câu hỏi sau:
Tại sao hình chiếu trục đo thường thể hiện nhiều mặt của vật thể hơn so với hình chiếu vuông góc?
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Hình chiếu trục đo thường thể hiện nhiều mặt của vật thể hơn so với hình chiếu vuông góc vì trong hình chiếu vuông góc (tia chiếu vuông góc với mặt phẳng chiếu), sẽ có các điểm, các đường thẳng trùng nhau (hay bị khuất) do hướng nhìn vuông góc, trong khi ở hình chiếu trục đo (tia chiếu song song với mặt phẳng chiếu), sẽ có nhiều điểm, đường thẳng không bị che khuất nên thể hiện nhiều mặt của vật thể hơn.
Xoay một hình lập phương để có thể quan sát được cả ba mặt của nó. Khi đó các thành phần quan sát được của hình lập phương có tạo thành hình chiếu trục đo của nó hay không? Hãy giải thích tại sao.
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Các phần quan sát được của hình lập phương có tạo thành hình chiếu trục đo của nó. Vì đây là hình chiếu song song của hình lập phương lên một mặt phẳng nào đó theo phương từ mắt ta qua vật thể rồi đến mặt phẳng không song song với bề mặt nào của hình lập phương.
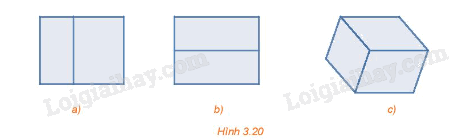
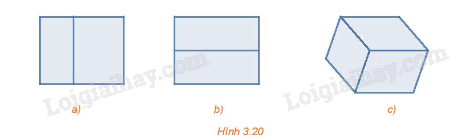
Trong các hình chiếu song song sau (H.3.20), hình nào thể hiện đúng hình chiếu trục đo của một hình hộp chữ nhật?
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Trong Hình 3.20a và 3.20b chỉ thấy được hai mặt của hình hộp chữ nhật nên không là hình chiếu trục đo của hình hộp chữ nhật. Trong Hình 3.20c có thể thấy được cả ba mặt của hình hộp chữ nhật nên hình này là hình chiếu trục đo của hình hộp chữ nhật.
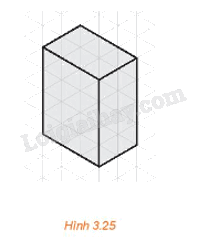
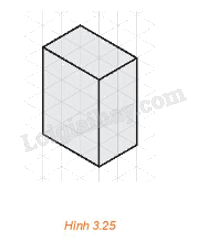
Hình chiếu trục đo của một hình hộp chữ nhật được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.25. Quy ước độ dài mỗi cạnh của tam giác đều là 10 mm, xác định kích thước mỗi chiều của hình hộp đó.
Phương pháp giải:
Quan sát hình 3.25 để trả lời
Lời giải chi tiết:
Chiều dài của hình hộp là: 3 . 10 = 30 (mm).
Chiều rộng của hình hộp là: 2 . 10 = 20 (mm).
Chiều cao của hình hộp là: 4 . 10 = 40 (mm).
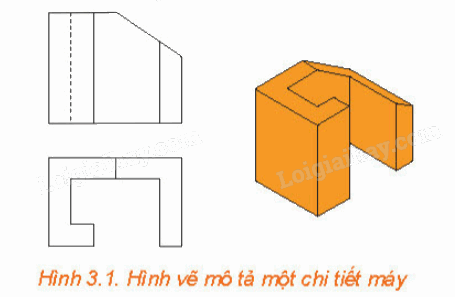
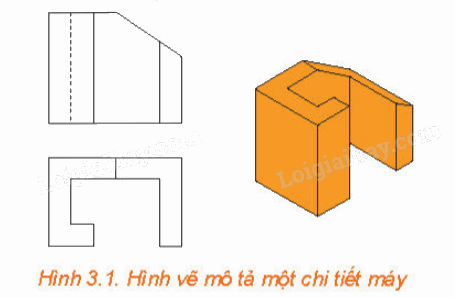
Hãy quan sát hình ảnh mở đầu (H.3.1) và cho biết hình nào là hình chiếu trục đo vuông góc đều của vật thể.
Phương pháp giải:
Trong hình chiếu trục đo vuông góc đều có:
- Mặt phẳng chiếu (P) vuông góc với phương chiếu l;
- Các góc trục đo đều bằng 120o.
- Các hệ số biến dạng đều bằng 1.
Lời giải chi tiết:
Hình màu cam trong Hình 3.1 là hình chiếu trục đo vuông góc đều của vật thể.
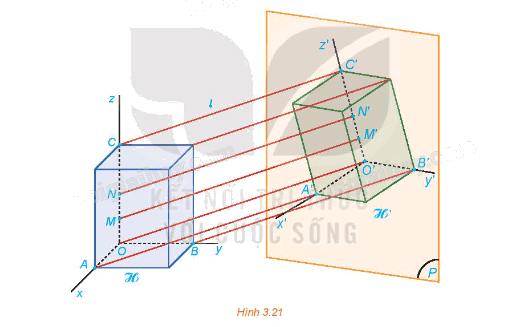
: Giả sử hình hộp chữ nhật ℋ trong HĐ5 được gắn thêm các trục Ox, Oy, Oz đôi một vuông góc dọc theo chiều dài, chiều rộng và chiều cao của ℋ. Gọi O'x', O'y' và O'z' lần lượt là hình chiếu của các trục đó lên mặt phẳng (P) theo phương l (H.3.21). a) Hình chiếu của các góc \(\widehat {xOy},\,\widehat {yOz},\,\widehat {zOx}\) là các góc nào trên mặt phẳng hình chiếu?
b) Giả sử M, N là hai điểm thuộc trục Oz và M', N' là hình chiếu tương ứng thuộc trục O'z'. So sánh hai tỉ số \(\frac{{O'M'}}{{OM}}\) và \(\frac{{O'N'}}{{ON}}\) .
Phương pháp giải:
Quan sát hình 3.121 để trả lời
Lời giải chi tiết:
a) Hình chiếu của các góc \(\widehat {xOy},\,\widehat {yOz},\,\widehat {zOx}\) lần lượt là các góc \(\widehat {x'O'y'},\,\widehat {y'O'z'},\,\widehat {z'O'x'}\) trên mặt phẳng hình chiếu.
b) Ta có: OO’ // MM' // NN'.
Suy ra \(\frac{{O'M'}}{{O'N'}} = \frac{{OM}}{{ON}}\) , do đó \(\frac{{O'M'}}{{OM}}\; = \frac{{O'N'}}{{ON}}\).
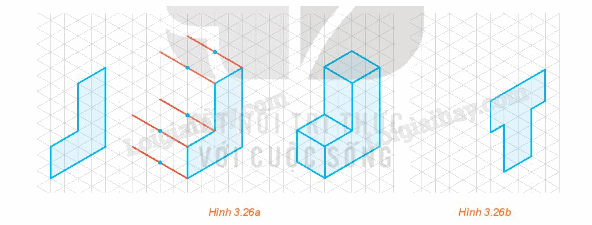
Hình 3.26a thể hiện cách vẽ dạng nổi của chữ cái “L” trên giấy kẻ ô tam giác đều. Hình nhận được là một hình chiếu trục đo vuông góc đều. Bằng cách tương tự hãy vẽ dạng nổi của chữ cái “T” (H.3.26b).
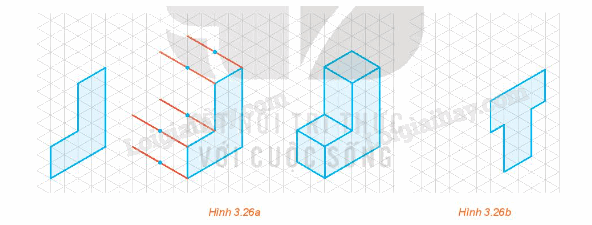
Phương pháp giải:
Quan sát hình 3.26 để trả lời
Lời giải chi tiết:
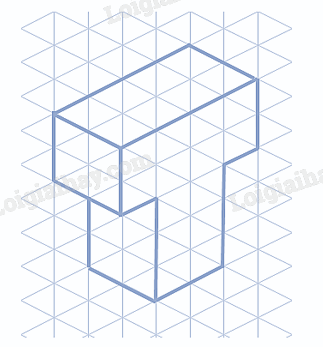
Ta vẽ được dạng nổi của chữ cái “T” như sau:
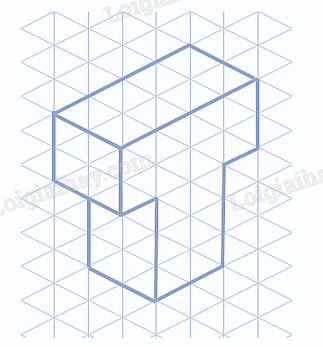
Cho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz đôi một vuông góc. Xét phép chiếu vuông góc lên mặt phẳng (P) đi qua O sao cho các trục Ox, Oy, Oz tạo với (P) các góc bằng nhau (H.3.23a). Gọi A', B', C' lần lượt là hình chiếu của A, B, C.
a) Chứng minh rằng ABC là tam giác đều.
b) Giải thích tại sao các khoảng cách từ A, B, C đến (P) bằng nhau, từ đó suy ra mặt phẳng (ABC) song song với mặt phẳng (P).
c) Gọi I là tâm tam giác đều ABC. Giải thích tại sao \(\widehat {A'OB'} = \widehat {AIB}\), từ đó suy ra \(\widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'} = 120^\circ \)
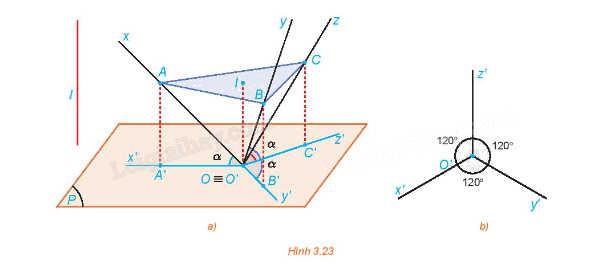
Phương pháp giải:
Tam giác đều là tam giác có 3 cạnh hoặc 3 góc bằng nhau.
Lời giải chi tiết:
a) Ta có: OA = OB = OC, \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \).
Suy ra các tam giác AOB, BOC và COA bằng nhau từng đôi một.
Từ đó suy ra AB = BC = CA nên tam giác ABC là tam giác đều.
b) Ta có: OA = OB = OC; \(\widehat {AA'O} = \widehat {BB'O} = \widehat {CC'O} = 90^\circ ;\widehat {\,AOA'} = \widehat {BOB'} = \widehat {COC'} = \alpha \)
Do đó, các tam giác AA'O, BB'O và CCO' bằng nhau từng đôi một.
Từ đó suy ra AA' = BB' = CC'.
Do đó, khoảng cách từ A, B, C đến (P) bằng nhau.
Ta có: AA' = BB', AA' // BB' nên ABB'A' là hình bình hành.
Suy ra: AB // A'B'.
Tương tự ta chứng minh BC // B'C'; CA // C'A'
Mà A'B', B'C', C'A' thuộc (P)
Suy ra: (ABC) song song với (P).
c) Dễ dàng chứng minh được IA = O'A' (AIO'A' là hình bình hành).
Tương tự IB = O'B', AB = A'B'.
Do đó ∆IAB = ∆O'A'B' (c.c.c).
Suy ra \(\widehat {A'O'B'} = \widehat {AIB}\).
Tương tự, ta chứng minh được \(\widehat {A'O'C'} = \widehat {CIA};\,\widehat {B'O'C'} = \widehat {BIC}.\)
Do I là tâm tam giác đều ABC nên dễ dàng chứng minh được \(\widehat {AIB} = \widehat {BIC} = \widehat {CIA} = 120^\circ \).
Nên suy ra \(\widehat {AIB} = \widehat {BIC} = \widehat {CIA} = \widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'}\).
Vậy \(\widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'} = 120^\circ \).
Cho hình hộp chữ nhật ℋ. Quan sát hình chiếu song song ℋ ' của hình ℋ lên mặt phẳng (P) theo phương l (H.3.17) và trả lời các câu hỏi sau:
a) Hình ℋ ' có phải là hình chiếu đứng, hình chiếu bằng hay hình chiếu cạnh của hình ℋ hay không?
b) Phương chiếu l có song song với mặt nào của hình hộp chữ nhật ℋ hay không?
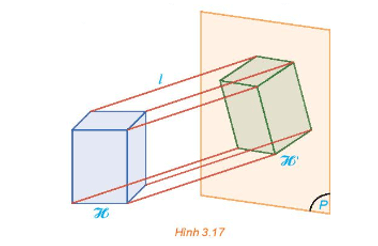
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
a) Hình ℋ ' không là hình chiếu đứng, hình chiếu bằng hay hình chiếu cạnh của hình ℋ vì hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh là các hình chiếu vuông góc của hình ℋ lên các mặt phẳng chiếu tương ứng.
b) Phương chiếu l không song song với mặt nào của hình hộp chữ nhật ℋ .
Hình chiếu trục đo của một hình hộp chữ nhật được cho như trong Hình 3.22b. Biết các hệ số biến dạng là p = 1, q = r = 0,5. Tính kích thước thực tế của hình hộp chữ nhật đó.
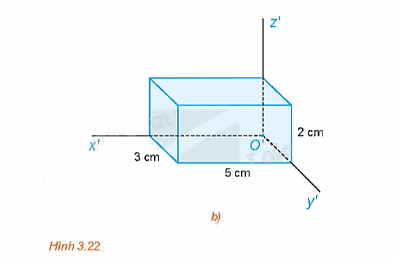
Phương pháp giải:
Các tỉ số \(p = \frac{{O'A'}}{{OA}},q = \frac{{O'B'}}{{OB}},r = \frac{{O'C'}}{{OC}}\) lần lượt là hệ số biến dạng theo trục \(O'x';\,\,O'y';\,\,O'z'\).
Lời giải chi tiết:
Gọi O, A, B, C là các đỉnh của hình hộp chữ nhật.
Ta có O' hình chiếu trục đo của O.
Gọi A', B', C' lần lượt là hình chiếu trục đo của A, B, C trên O'x', O'y', O'z'.
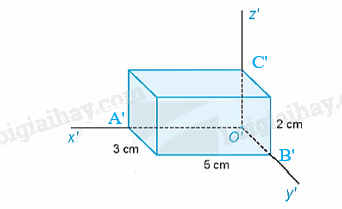
Ta có: \(p = \frac{{O'A'}}{{OA}} = 1\), mà O'A' = 5 cm nên OA = O'A' = 5 cm.
\(q = \frac{{O'B'}}{{OB}} = 0,5\), mà O'B' = 3 cm nên \(OB = \frac{{O'B'}}{{0,5}} = \frac{3}{{0,5}} = 6\)cm
\(r = \frac{{O'C'}}{{OC}} = 0,5\), mà O'C' = 2 cm nên OC = \(\frac{{O'C'}}{{0,5}} = \frac{2}{{0,5}} = 4\)cm
Cho hình hộp chữ nhật ℋ. Quan sát hình chiếu song song ℋ ' của hình ℋ lên mặt phẳng (P) theo phương l (H.3.17) và trả lời các câu hỏi sau:
a) Hình ℋ ' có phải là hình chiếu đứng, hình chiếu bằng hay hình chiếu cạnh của hình ℋ hay không?
b) Phương chiếu l có song song với mặt nào của hình hộp chữ nhật ℋ hay không?
Phương pháp giải:
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết:
a) Hình ℋ ' không là hình chiếu đứng, hình chiếu bằng hay hình chiếu cạnh của hình ℋ vì hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh là các hình chiếu vuông góc của hình ℋ lên các mặt phẳng chiếu tương ứng.
b) Phương chiếu l không song song với mặt nào của hình hộp chữ nhật ℋ .
Tại sao hình chiếu trục đo thường thể hiện nhiều mặt của vật thể hơn so với hình chiếu vuông góc?
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Hình chiếu trục đo thường thể hiện nhiều mặt của vật thể hơn so với hình chiếu vuông góc vì trong hình chiếu vuông góc (tia chiếu vuông góc với mặt phẳng chiếu), sẽ có các điểm, các đường thẳng trùng nhau (hay bị khuất) do hướng nhìn vuông góc, trong khi ở hình chiếu trục đo (tia chiếu song song với mặt phẳng chiếu), sẽ có nhiều điểm, đường thẳng không bị che khuất nên thể hiện nhiều mặt của vật thể hơn.
Trong các hình chiếu song song sau (H.3.20), hình nào thể hiện đúng hình chiếu trục đo của một hình hộp chữ nhật?
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Trong Hình 3.20a và 3.20b chỉ thấy được hai mặt của hình hộp chữ nhật nên không là hình chiếu trục đo của hình hộp chữ nhật. Trong Hình 3.20c có thể thấy được cả ba mặt của hình hộp chữ nhật nên hình này là hình chiếu trục đo của hình hộp chữ nhật.
Xoay một hình lập phương để có thể quan sát được cả ba mặt của nó. Khi đó các thành phần quan sát được của hình lập phương có tạo thành hình chiếu trục đo của nó hay không? Hãy giải thích tại sao.
Phương pháp giải:
Hình chiếu song song của một hình H lên mặt phẳng (P) theo phương l không song song với bề mặt nào của hình H được gọi là hình chiếu trục đo của H.
Lời giải chi tiết:
Các phần quan sát được của hình lập phương có tạo thành hình chiếu trục đo của nó. Vì đây là hình chiếu song song của hình lập phương lên một mặt phẳng nào đó theo phương từ mắt ta qua vật thể rồi đến mặt phẳng không song song với bề mặt nào của hình lập phương.
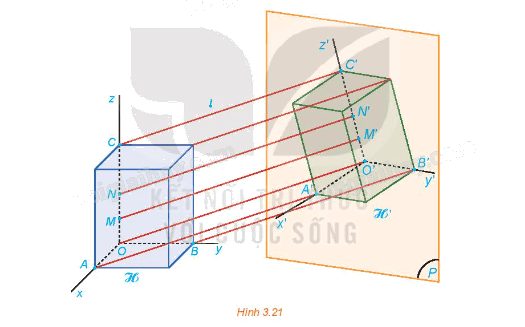
: Giả sử hình hộp chữ nhật ℋ trong HĐ5 được gắn thêm các trục Ox, Oy, Oz đôi một vuông góc dọc theo chiều dài, chiều rộng và chiều cao của ℋ. Gọi O'x', O'y' và O'z' lần lượt là hình chiếu của các trục đó lên mặt phẳng (P) theo phương l (H.3.21). a) Hình chiếu của các góc \(\widehat {xOy},\,\widehat {yOz},\,\widehat {zOx}\) là các góc nào trên mặt phẳng hình chiếu?
b) Giả sử M, N là hai điểm thuộc trục Oz và M', N' là hình chiếu tương ứng thuộc trục O'z'. So sánh hai tỉ số \(\frac{{O'M'}}{{OM}}\) và \(\frac{{O'N'}}{{ON}}\) .
Phương pháp giải:
Quan sát hình 3.121 để trả lời
Lời giải chi tiết:
a) Hình chiếu của các góc \(\widehat {xOy},\,\widehat {yOz},\,\widehat {zOx}\) lần lượt là các góc \(\widehat {x'O'y'},\,\widehat {y'O'z'},\,\widehat {z'O'x'}\) trên mặt phẳng hình chiếu.
b) Ta có: OO’ // MM' // NN'.
Suy ra \(\frac{{O'M'}}{{O'N'}} = \frac{{OM}}{{ON}}\) , do đó \(\frac{{O'M'}}{{OM}}\; = \frac{{O'N'}}{{ON}}\).
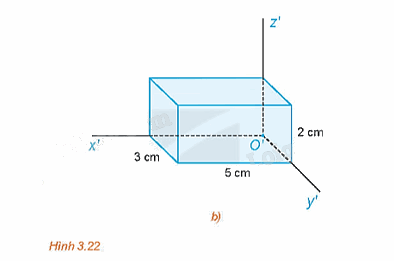
Hình chiếu trục đo của một hình hộp chữ nhật được cho như trong Hình 3.22b. Biết các hệ số biến dạng là p = 1, q = r = 0,5. Tính kích thước thực tế của hình hộp chữ nhật đó.
Phương pháp giải:
Các tỉ số \(p = \frac{{O'A'}}{{OA}},q = \frac{{O'B'}}{{OB}},r = \frac{{O'C'}}{{OC}}\) lần lượt là hệ số biến dạng theo trục \(O'x';\,\,O'y';\,\,O'z'\).
Lời giải chi tiết:
Gọi O, A, B, C là các đỉnh của hình hộp chữ nhật.
Ta có O' hình chiếu trục đo của O.
Gọi A', B', C' lần lượt là hình chiếu trục đo của A, B, C trên O'x', O'y', O'z'.
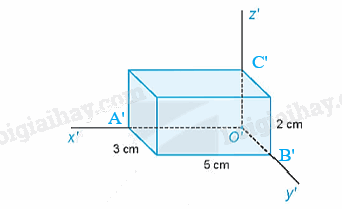
Ta có: \(p = \frac{{O'A'}}{{OA}} = 1\), mà O'A' = 5 cm nên OA = O'A' = 5 cm.
\(q = \frac{{O'B'}}{{OB}} = 0,5\), mà O'B' = 3 cm nên \(OB = \frac{{O'B'}}{{0,5}} = \frac{3}{{0,5}} = 6\)cm
\(r = \frac{{O'C'}}{{OC}} = 0,5\), mà O'C' = 2 cm nên OC = \(\frac{{O'C'}}{{0,5}} = \frac{2}{{0,5}} = 4\)cm
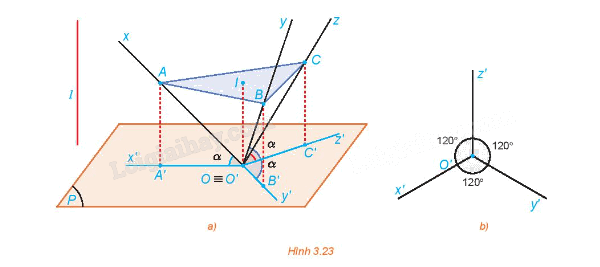
Cho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz đôi một vuông góc. Xét phép chiếu vuông góc lên mặt phẳng (P) đi qua O sao cho các trục Ox, Oy, Oz tạo với (P) các góc bằng nhau (H.3.23a). Gọi A', B', C' lần lượt là hình chiếu của A, B, C.
a) Chứng minh rằng ABC là tam giác đều.
b) Giải thích tại sao các khoảng cách từ A, B, C đến (P) bằng nhau, từ đó suy ra mặt phẳng (ABC) song song với mặt phẳng (P).
c) Gọi I là tâm tam giác đều ABC. Giải thích tại sao \(\widehat {A'OB'} = \widehat {AIB}\), từ đó suy ra \(\widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'} = 120^\circ \)
Phương pháp giải:
Tam giác đều là tam giác có 3 cạnh hoặc 3 góc bằng nhau.
Lời giải chi tiết:
a) Ta có: OA = OB = OC, \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \).
Suy ra các tam giác AOB, BOC và COA bằng nhau từng đôi một.
Từ đó suy ra AB = BC = CA nên tam giác ABC là tam giác đều.
b) Ta có: OA = OB = OC; \(\widehat {AA'O} = \widehat {BB'O} = \widehat {CC'O} = 90^\circ ;\widehat {\,AOA'} = \widehat {BOB'} = \widehat {COC'} = \alpha \)
Do đó, các tam giác AA'O, BB'O và CCO' bằng nhau từng đôi một.
Từ đó suy ra AA' = BB' = CC'.
Do đó, khoảng cách từ A, B, C đến (P) bằng nhau.
Ta có: AA' = BB', AA' // BB' nên ABB'A' là hình bình hành.
Suy ra: AB // A'B'.
Tương tự ta chứng minh BC // B'C'; CA // C'A'
Mà A'B', B'C', C'A' thuộc (P)
Suy ra: (ABC) song song với (P).
c) Dễ dàng chứng minh được IA = O'A' (AIO'A' là hình bình hành).
Tương tự IB = O'B', AB = A'B'.
Do đó ∆IAB = ∆O'A'B' (c.c.c).
Suy ra \(\widehat {A'O'B'} = \widehat {AIB}\).
Tương tự, ta chứng minh được \(\widehat {A'O'C'} = \widehat {CIA};\,\widehat {B'O'C'} = \widehat {BIC}.\)
Do I là tâm tam giác đều ABC nên dễ dàng chứng minh được \(\widehat {AIB} = \widehat {BIC} = \widehat {CIA} = 120^\circ \).
Nên suy ra \(\widehat {AIB} = \widehat {BIC} = \widehat {CIA} = \widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'}\).
Vậy \(\widehat {A'O'B'} = \widehat {B'O'C'} = \widehat {A'O'C'} = 120^\circ \).
Hãy quan sát hình ảnh mở đầu (H.3.1) và cho biết hình nào là hình chiếu trục đo vuông góc đều của vật thể.
Phương pháp giải:
Trong hình chiếu trục đo vuông góc đều có:
- Mặt phẳng chiếu (P) vuông góc với phương chiếu l;
- Các góc trục đo đều bằng 120o.
- Các hệ số biến dạng đều bằng 1.
Lời giải chi tiết:
Hình màu cam trong Hình 3.1 là hình chiếu trục đo vuông góc đều của vật thể.
Hình chiếu trục đo của một hình hộp chữ nhật được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.25. Quy ước độ dài mỗi cạnh của tam giác đều là 10 mm, xác định kích thước mỗi chiều của hình hộp đó.
Phương pháp giải:
Quan sát hình 3.25 để trả lời
Lời giải chi tiết:
Chiều dài của hình hộp là: 3 . 10 = 30 (mm).
Chiều rộng của hình hộp là: 2 . 10 = 20 (mm).
Chiều cao của hình hộp là: 4 . 10 = 40 (mm).
Hình 3.26a thể hiện cách vẽ dạng nổi của chữ cái “L” trên giấy kẻ ô tam giác đều. Hình nhận được là một hình chiếu trục đo vuông góc đều. Bằng cách tương tự hãy vẽ dạng nổi của chữ cái “T” (H.3.26b).
Phương pháp giải:
Quan sát hình 3.26 để trả lời
Lời giải chi tiết:
Ta vẽ được dạng nổi của chữ cái “T” như sau:
Mục 4 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường xoay quanh các chủ đề quan trọng như đạo hàm, ứng dụng đạo hàm trong việc khảo sát hàm số, hoặc các bài toán về tối ưu hóa. Việc nắm vững kiến thức trong mục này là nền tảng cho các chương trình học tiếp theo và các kỳ thi quan trọng.
Để hiểu rõ hơn về Mục 4, chúng ta cần xem xét các nội dung chính sau:
Dưới đây là phần giải chi tiết các bài tập trong Mục 4, trang 59, 60, 61, 62, 63, 64 của sách Toán 11 - Kết nối tri thức:
Bài 1: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 2: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 3: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 4: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 5: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 6: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 7: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 8: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 9: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 10: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 11: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Bài 12: (Đề bài)... Giải: (Các bước giải chi tiết, kèm theo giải thích)...
Để giải các bài tập trong Mục 4 một cách hiệu quả, bạn nên:
Việc hiểu rõ Mục 4 không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 11 và các chương trình học tiếp theo. Đạo hàm và ứng dụng của nó là một trong những chủ đề quan trọng nhất trong Toán học, và việc nắm vững kiến thức này sẽ giúp bạn thành công trong học tập và công việc.
| Hàm số y = f(x) | Đạo hàm y' = f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |
Hy vọng với những hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải các bài tập trong Mục 4 trang 59, 60, 61, 62, 63, 64 Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc bạn học tốt!