Bài 1.5 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và áp dụng linh hoạt vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.5 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ nào?
Đề bài
Trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ nào? (Gợi ý: Tính vectơ tịnh tiến đó theo hai vectơ \(\overrightarrow u ,\overrightarrow v \) trên hình vẽ).

Phương pháp giải - Xem chi tiết
Tính vectơ tịnh tiến đó theo hai vectơ \(\overrightarrow u ,\overrightarrow v \) trên hình vẽ
Lời giải chi tiết
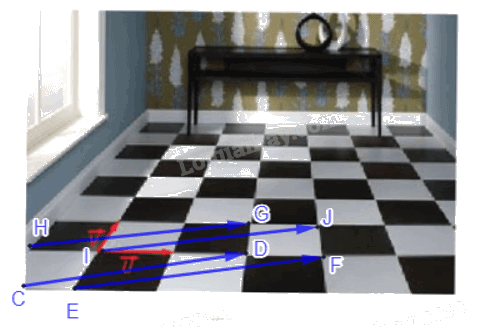
Đặt các điểm như hình vẽ trên. Viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là viên gạch GDFJ, viên gạch ở góc dưới bên trái là viên gạch HCEI.
Theo quy tắc hình bình hành, ta suy ra \(\overrightarrow {IJ} = \vec v + 3\vec u\). Đặt \(\vec x = \vec v + 3\vec u\).
Phép tịnh tiến \({T_{\vec x}}\) biến các điểm H, C, E, I tương ứng thành các điểm G, D, F, J. Do đó, phép tịnh tiến \({T_{\vec x}}\) biến viên gạch HCEI thành viên gạch GDFJ.
Vậy trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ \(\vec x\) với \(\vec x = \vec v + 3\vec u\)
Bài 1.5 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh tìm số hạng tổng quát của dãy số và xác định xem dãy số đó có phải là cấp số cộng hay cấp số nhân hay không. Để giải bài tập này, chúng ta cần nắm vững các khái niệm và công thức liên quan đến dãy số, cấp số cộng và cấp số nhân.
Cho dãy số (un) được xác định bởi:
a) Tìm số hạng tổng quát un.
b) Chứng minh rằng dãy số (un) không phải là cấp số cộng.
c) Chứng minh rằng dãy số (un) không phải là cấp số nhân.
a) Tìm số hạng tổng quát un:
Ta có:
Nhận thấy un = 3 * 2n-1 - 1. Ta sẽ chứng minh bằng quy nạp.
Bước 1: Kiểm tra với n = 1
u1 = 3 * 21-1 - 1 = 3 * 1 - 1 = 2 (đúng)
Bước 2: Giả sử mệnh đề đúng với n = k
uk = 3 * 2k-1 - 1
Bước 3: Chứng minh mệnh đề đúng với n = k+1
uk+1 = 2uk + 1 = 2(3 * 2k-1 - 1) + 1 = 3 * 2k - 2 + 1 = 3 * 2k - 1 = 3 * 2(k+1)-1 - 1
Vậy, số hạng tổng quát của dãy số là un = 3 * 2n-1 - 1.
b) Chứng minh rằng dãy số (un) không phải là cấp số cộng:Để dãy số (un) là cấp số cộng, hiệu giữa hai số hạng liên tiếp phải là một hằng số.
Ta có:
Vì u2 - u1 ≠ u3 - u2, nên dãy số (un) không phải là cấp số cộng.
c) Chứng minh rằng dãy số (un) không phải là cấp số nhân:Để dãy số (un) là cấp số nhân, tỉ số giữa hai số hạng liên tiếp phải là một hằng số.
Ta có:
Vì u2 / u1 ≠ u3 / u2, nên dãy số (un) không phải là cấp số nhân.
Vậy, ta đã tìm được số hạng tổng quát của dãy số (un) là un = 3 * 2n-1 - 1 và chứng minh được rằng dãy số (un) không phải là cấp số cộng cũng như không phải là cấp số nhân.
Để hiểu sâu hơn về dãy số, cấp số cộng và cấp số nhân, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến dãy số, cấp số cộng và cấp số nhân.