Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 1.11 trang 20 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải toán khoa học, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
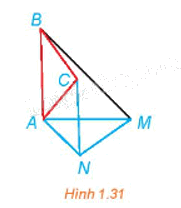
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
Đề bài
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
Phương pháp giải - Xem chi tiết
Ta cần tìm tâm và góc quay: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết
Tam giác BAM vuông cân tại A nên AB = AM và \(\widehat {BAM} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm A thành điểm A, biến điểm B thành điểm M (1).
Tam giác ACN vuông cân tại A nên AC = AN và \(\widehat {CAN} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm C thành điểm N (2).
Từ (1) và (2) suy ra phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến tam giác ABC thành tam giác AMN.
Bài 1.11 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về tập xác định, tập giá trị, tính đơn điệu và cực trị của hàm số.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 1.11 thường yêu cầu học sinh:
Để giải bài 1.11 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta có thể áp dụng các phương pháp sau:
(Giả sử đề bài cụ thể là: Cho hàm số y = x2 - 4x + 3. Tìm tập xác định, tập giá trị, điểm cực tiểu và vẽ đồ thị hàm số.)
1. Tập xác định: Hàm số y = x2 - 4x + 3 là hàm số bậc hai, xác định trên tập số thực R.
2. Tập giá trị: Hàm số có dạng parabol với hệ số a = 1 > 0, do đó hàm số đạt giá trị nhỏ nhất tại đỉnh parabol. Hoành độ đỉnh là x = -b/2a = -(-4)/(2*1) = 2. Tung độ đỉnh là y = 22 - 4*2 + 3 = -1. Vậy tập giá trị của hàm số là [-1, +∞).
3. Điểm cực tiểu: Hàm số đạt giá trị nhỏ nhất tại điểm (2, -1). Đây là điểm cực tiểu của hàm số.
4. Vẽ đồ thị:
Ví dụ: Sử dụng đồ thị hàm số y = x2 - 4x + 3 để giải phương trình x2 - 4x + 3 = 0.
Lời giải: Phương trình x2 - 4x + 3 = 0 tương đương với việc tìm các giao điểm của đồ thị hàm số y = x2 - 4x + 3 với trục Ox. Dựa vào đồ thị, ta thấy đồ thị cắt trục Ox tại hai điểm có hoành độ x = 1 và x = 3. Vậy phương trình có hai nghiệm là x = 1 và x = 3.
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Hãy chú trọng vào việc phân tích đề bài, lựa chọn phương pháp giải phù hợp và kiểm tra lại kết quả.
Bài 1.11 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về hàm số và đồ thị. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.