Giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng khám phá lời giải chi tiết của bài 1.13 này ngay bây giờ!

Cho hình bình hành ABCD với tâm O.

Đề bài

Cho hình bình hành ABCD với tâm O.

a) Tìm ảnh của đường thẳng AB qua phép đối xứng tâm O.

b) Tìm ảnh của tam giác ABC qua phép đối xứng tâm O.

Phương pháp giải - Xem chi tiết Giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 1

- Tìm ảnh của từng điểm A, B, C qua phép đối xứng tâm O. Sau đó nối chúng với nhau ta được ảnh của AB, tam giác ABC qua phép đối xứng tâm O.

- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứng tâm O . Điểm O được gọi là tâm đối xứng.

Lời giải chi tiết

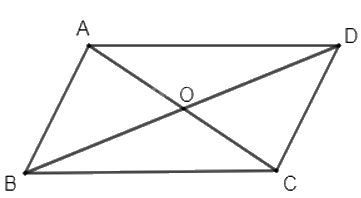
Giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Vì ABCD là hình bình hành nên tâm O là trung điểm các đường chéo AC và BD.

Vì O là trung điểm của AC nên C là ảnh của A qua phép đối xứng tâm O.

Vì O là trung điểm của BD nên D là ảnh của B qua phép đối xứng tâm O.

Do đó, CD là ảnh của đường thẳng AB qua phép đối xứng tâm O.

Lại có A là ảnh của C qua phép đối xứng tâm O. Vậy tam giác CDA là ảnh của tam giác ABC qua phép đối xứng tâm O.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng soạn toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm đạo hàm và sử dụng đạo hàm để khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:

Định nghĩa đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì và cách tính đạo hàm bằng định nghĩa.
Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm số đa thức, hàm số lượng giác, hàm số mũ và hàm số logarit.
Ứng dụng của đạo hàm: Sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu và điểm uốn của hàm số.

Lời giải chi tiết bài 1.13 trang 20

Để giải bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta thực hiện các bước sau:

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp nhất của hàm số.
Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
Khảo sát tính đơn điệu: Xét dấu đạo hàm trên các khoảng xác định để xác định khoảng đồng biến và nghịch biến của hàm số.
Tìm điểm uốn: Tính đạo hàm cấp hai và giải phương trình đạo hàm cấp hai bằng 0 để tìm các điểm uốn của hàm số.
Khảo sát tính lồi lõm: Xét dấu đạo hàm cấp hai trên các khoảng xác định để xác định khoảng lồi và khoảng lõm của hàm số.
Vẽ đồ thị hàm số: Dựa vào các kết quả khảo sát để vẽ đồ thị hàm số.

Ví dụ minh họa

Giả sử hàm số cần khảo sát là y = x³ - 3x² + 2. Chúng ta sẽ thực hiện các bước sau:

Tính đạo hàm cấp nhất: y' = 3x² - 6x
Tìm điểm cực trị: Giải phương trình 3x² - 6x = 0, ta được x = 0 và x = 2.
Khảo sát tính đơn điệu:
- Khi x < 0, y' > 0, hàm số đồng biến.
- Khi 0 < x < 2, y' < 0, hàm số nghịch biến.
- Khi x > 2, y' > 0, hàm số đồng biến.
Tính đạo hàm cấp hai: y'' = 6x - 6
Tìm điểm uốn: Giải phương trình 6x - 6 = 0, ta được x = 1.
Khảo sát tính lồi lõm:
- Khi x < 1, y'' < 0, hàm số lõm.
- Khi x > 1, y'' > 0, hàm số lồi.

Lưu ý khi giải bài tập

Khi giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn cần lưu ý những điều sau:

Đọc kỹ đề bài và xác định chính xác yêu cầu của bài toán.
Sử dụng đúng các quy tắc tính đạo hàm và các công thức liên quan.
Kiểm tra lại kết quả tính toán để đảm bảo tính chính xác.
Vẽ đồ thị hàm số để minh họa kết quả khảo sát.

Tổng kết

Bài 1.13 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.