Bài 1.27 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0\)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0\) và hai điểm \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right),{\rm{ }}B\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
a) Tìm tọa độ điểm \(A'\) là ảnh của điểm A qua phép đối xứng trục \(\Delta \)
b) Xác định điểm M thuộc đường thẳng \(\Delta \) sao cho MA + MB đạt giá trị nhỏ nhất.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học về phép đối xứng trục để làm
Lời giải chi tiết
a) Ta có: \(2{\rm{ }}.{\rm{ }}\left( {-{\rm{ }}1} \right){\rm{ }}-{\rm{ }}2{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}-{\rm{ }}5{\rm{ }} \ne {\rm{ }}0\) nên \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right)\) không thuộc ∆.
Gọi H là chân đường vuông góc hạ từ A xuống ∆.
Vì H thuộc ∆ nên \(H\left( {x;2x-1} \right)\). Ta có: \(\overrightarrow {AH} = (x + 1;2x - 3)\), vectơ chỉ phương của đường thẳng ∆ là \(\overrightarrow {{u_\Delta }} = \left( {1;\,2} \right)\)
Vì AH vuông góc với ∆ nên \(\overrightarrow {AH} .\overrightarrow {{u_\Delta }} = 0 \Leftrightarrow \left( {x + 1} \right).1 + \left( {2x - 3} \right).2 = 0 \Rightarrow x = 1\)
Từ đó suy ra H(1; 1).
Vì A' là ảnh của điểm A qua phép đối xứng trục ∆ nên AA' vuông góc với ∆ tại H và H là trung điểm của AA'.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2.1 - \left( { - 1} \right) = 3}\\{{y_{A'}} = 2{y_H} - {y_A} = 2.1 - 2 = 0}\end{array}} \right.\)
Vậy A'(3; 0).
b)
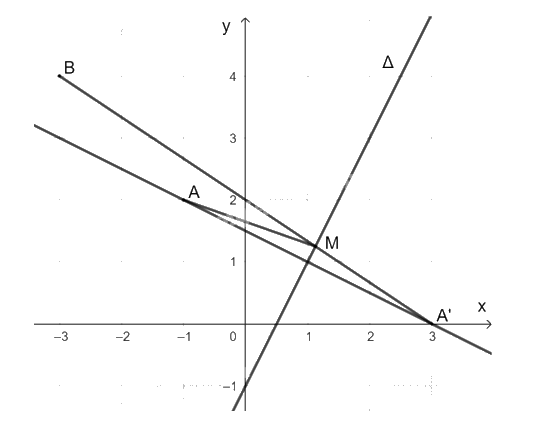
Ta có: \(2.\left( {-3} \right)-4-1{\rm{ }} = -11;{\rm{ 2}}.\left( {-1} \right)-2-1 = -5\) và \(\left( {-11} \right).\left( {-5} \right) = 55 > 0\)nên hai điểm A và B nằm về một phía của đường thẳng ∆.
Vì M thuộc \(\Delta \) và A và A' đối xứng nhau qua \(\Delta \) nên MA = MA' và A' và B nằm về hai phía của đường thẳng \(\Delta \).
Do đó, MA + MB = MA' + MB đạt giá trị nhỏ nhất khi M là giao điểm của A'B và \(\Delta \).
Ta có: \(\overrightarrow {A'B} = ( - 6;4)\), suy ra \(\overrightarrow {{n_{A'B}}} = (2;3)\) là một vectơ pháp tuyến của đường thẳng A'B. Phương trình đường thẳng A'B là \(2\left( {x-3} \right) + 3\left( {y-0} \right) = 0\) hay \(2x + 3y-6 = 0.\)
Tọa độ giao điểm M của A'B và ∆ là nghiệm của hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{2x - y - 1 = 0}\\{2x + 3y - 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{9}{8}}\\{y = \frac{5}{4}}\end{array}} \right.} \right.\)
Vậy \(M\left( {\frac{9}{8};\,\frac{5}{4}} \right)\).
Bài 1.27 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như đạo hàm, cực trị, và khoảng đơn điệu của hàm số.
Bài tập 1.27 thường có dạng yêu cầu học sinh:
Để giải bài 1.27 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta thực hiện theo các bước sau:
Giả sử hàm số cần khảo sát là y = x3 - 3x2 + 2. Ta thực hiện các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Việc giải bài tập 1.27 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức không chỉ giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề và tư duy logic. Đây là những kỹ năng cần thiết cho việc học tập và làm việc trong tương lai.
Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể tự tin giải bài tập 1.27 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức. Hãy tiếp tục luyện tập và khám phá thêm nhiều bài tập thú vị khác tại giaitoan.edu.vn!