Bài 2.28 trang 51 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học. Bài tập này thường yêu cầu vận dụng các công thức và định lý đã được trình bày trong chuyên đề.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 2.28 này, giúp các em học sinh có thể tự học và nắm vững kiến thức một cách hiệu quả.
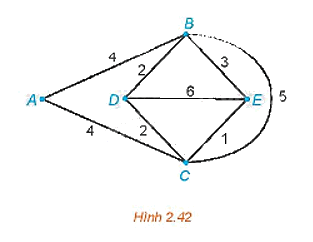
Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.42.
Đề bài
Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.42.
Phương pháp giải - Xem chi tiết
Dựa vào bài toán người đưa thư để làm
Lời giải chi tiết
Đồ thị Hình 2.42 chỉ có hai đỉnh bậc lẻ là D và E nên ta có thể tìm được một đường đi Euler từ D đến E (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ D đến E là DBACDEBCE và tổng độ dài của nó là
2 + 4 + 4 + 2 + 6 + 3 + 5 + 1 = 27.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến D theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ E đến D là ECD và có độ dài là 1 + 2 = 3.
Vậy một chu trình cần tìm là DBACDEBCECD và có độ dài là 27 + 3 = 30.
Bài 2.28 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài toán thuộc chủ đề về đạo hàm. Để giải bài toán này, học sinh cần nắm vững các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 2.28 thường yêu cầu tính đạo hàm của một hàm số hoặc tìm cực trị của hàm số. Việc xác định đúng yêu cầu của bài toán là bước đầu tiên quan trọng để giải bài toán thành công.
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 2.28. Giả sử bài toán yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1.
Bước 1: Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = (x3)' - (3x2)' + (2x)' + (1)'
Bước 2: Áp dụng quy tắc đạo hàm của lũy thừa, ta có:
(x3)' = 3x2
(3x2)' = 6x
(2x)' = 2
(1)' = 0
Bước 3: Thay các kết quả vào biểu thức f'(x), ta có:
f'(x) = 3x2 - 6x + 2
Vậy, đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1 là f'(x) = 3x2 - 6x + 2.
Để hiểu rõ hơn về cách tính đạo hàm, chúng ta có thể xem xét một số ví dụ minh họa khác. Ví dụ, tính đạo hàm của hàm số g(x) = sin(x) + cos(x). Áp dụng quy tắc đạo hàm của hàm lượng giác, ta có:
g'(x) = (sin(x))' + (cos(x))' = cos(x) - sin(x)
Ngoài ra, học sinh có thể tự giải các bài tập tương tự để rèn luyện kỹ năng tính đạo hàm. Ví dụ:
Bài 2.28 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và thực hành giải nhiều bài tập, học sinh có thể tự tin giải quyết các bài toán về đạo hàm một cách hiệu quả.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể hiểu rõ hơn về cách giải bài 2.28 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!