Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp bạn hiểu rõ hơn về kiến thức đã học.

Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 Kết nối tri thức đầy đủ, chính xác, giúp bạn tự học hiệu quả và đạt kết quả cao trong các kỳ thi.

Bản vẽ ở Hình 3.53 mô tả vật thể nào trong thực tế?

Đề bài

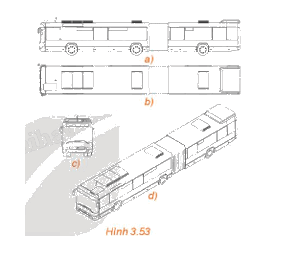
Bản vẽ ở Hình 3.53 mô tả vật thể nào trong thực tế? Cho biết hình nào là hình chiếu vuông góc, hình nào là hình chiếu trục đo của vật thể đó.

Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Hình biểu diễn H’ của một hình, khối H trong không gian là hình chiếu của H lên mặt phẳng qua một phép chiếu. Nếu phép chiếu là phép chiếu song song thì H’ là hình chiếu trục đo của H.

Lời giải chi tiết

Bản vẽ ở Hình 3.53 mô tả một chiếc xe buýt. Hình a, b, c là hình chiếu vuông góc; hình d là hình chiếu trục đo.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách bài tập Toán 11 trên nền tảng tài liệu toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức - Lời giải chi tiết

Bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm bậc nhất: Tính f'(x) để tìm các điểm dừng.
Tìm các điểm dừng: Giải phương trình f'(x) = 0 để tìm các giá trị x mà tại đó đạo hàm bằng 0.
Lập bảng biến thiên: Xác định dấu của đạo hàm trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến.
Kết luận về cực trị: Dựa vào bảng biến thiên để xác định các điểm cực đại, cực tiểu.

Lời giải chi tiết:

Giả sử hàm số cần khảo sát là f(x) = x³ - 3x² + 2 (ví dụ minh họa). Chúng ta sẽ áp dụng các bước trên để giải bài toán.

Bước 1: Tập xác định

Hàm số f(x) = x³ - 3x² + 2 có tập xác định là D = ℝ (tập hợp tất cả các số thực).

Bước 2: Tính đạo hàm bậc nhất

f'(x) = 3x² - 6x

Bước 3: Tìm các điểm dừng

Giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2 là các điểm dừng.

Bước 4: Lập bảng biến thiên

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	↗	↘	↗

Bước 5: Kết luận về cực trị

Dựa vào bảng biến thiên, ta thấy:

Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

Lưu ý: Đây chỉ là một ví dụ minh họa. Bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức có thể có hàm số khác. Bạn cần áp dụng các bước tương tự để giải bài toán cụ thể.

Việc hiểu rõ các khái niệm về đạo hàm, điểm dừng, khoảng đồng biến, nghịch biến và cực trị là rất quan trọng để giải quyết các bài toán về khảo sát hàm số. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng này.

Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.

Ngoài ra, bạn có thể tham khảo thêm các tài liệu sau: