Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.9 trang 44 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải toán khoa học, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
Đề bài
Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
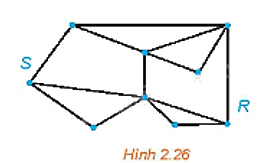
Phương pháp giải - Xem chi tiết
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết
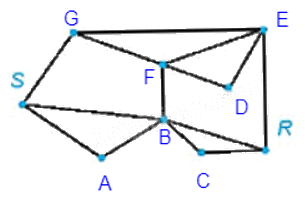
Đặt thêm tên các đỉnh vào đồ thị như hình vẽ trên.
Có thể thấy một chu trình Hamilton xuất phát từ đỉnh S của đồ thị G là SABCREDFGS.
Bài 2.9 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán hình học. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ chỉ phương, vectơ pháp tuyến, phương trình đường thẳng, phương trình mặt phẳng và các điều kiện song song, vuông góc giữa chúng.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, đề bài sẽ cho trước một số thông tin về các đường thẳng và mặt phẳng trong không gian, sau đó yêu cầu chúng ta tìm kiếm một số yếu tố như:
Để giải quyết bài tập về đường thẳng và mặt phẳng, chúng ta có thể áp dụng một số phương pháp sau:
(Nội dung lời giải chi tiết bài 2.9 trang 44 sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức, định lý liên quan. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm phương trình mặt phẳng chứa đường thẳng d và song song với mặt phẳng (P). Ta thực hiện như sau:
Ngoài bài 2.9, còn rất nhiều bài tập tương tự về đường thẳng và mặt phẳng trong không gian. Để nắm vững kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm các bài tập sau:
Khi giải bài tập về đường thẳng và mặt phẳng, bạn cần lưu ý một số điều sau:
Bài 2.9 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.