Bài 2.25 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
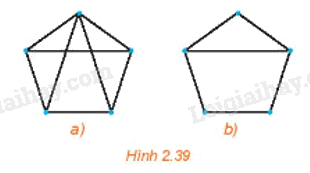
Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
Đề bài
Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
Phương pháp giải - Xem chi tiết
Định lí Ore: Nếu G là đơn đồ thị có n đỉnh \(\left( {n \ge 3} \right)\) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Lời giải chi tiết
Ta thấy hai đồ thị ở Hình 2.39 đều là đơn đồ thị và mỗi đồ thị đều có số đỉnh lớn hơn 3.
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
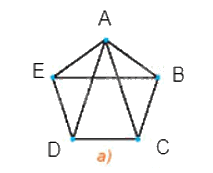
Đồ thị này có 5 đỉnh, các đỉnh đều có bậc là 3, trừ đỉnh A có bậc là 4 nên mỗi cặp đỉnh không kề nhau có tổng bậc nhỏ nhất là 6, mà 6 > 5, do đó đồ thị này thỏa mãn định lí Ore. Vậy đồ thị Hình 2.39 a) có một chu trình Hamilton.
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
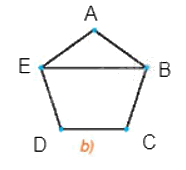
Đồ thị này có 5 đỉnh, đỉnh E và đỉnh B đều có bậc là 3, các đỉnh còn lại đều có bậc là 2 nên mỗi cặp đỉnh không kề nhau có tổng số bậc nhỏ nhất là 4 (chẳng hạn đỉnh A và đỉnh D), do đó đồ thị này không thỏa mãn định lí Ore. Tuy nhiên thì đồ thị này vẫn có chu trình Hamilton, một chu trình Hamilton của đồ thị là ABCDEA.
Do đó, ta khẳng định lại định lí Ore chỉ là một điều kiện đủ cho sự tồn tại của chu trình Hamilton.
Bài 2.25 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm điểm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đầu tiên, cần xác định rõ hàm số được đề cập trong bài toán và xác định tập xác định của hàm số đó. Việc này giúp chúng ta giới hạn phạm vi tìm kiếm các điểm cực trị và đảm bảo tính chính xác của kết quả.
Tiếp theo, chúng ta cần tính đạo hàm cấp một của hàm số. Đạo hàm cấp một đóng vai trò quan trọng trong việc xác định các điểm dừng của hàm số, tức là các điểm mà tại đó đạo hàm bằng không.
Sau khi tính được đạo hàm cấp một, chúng ta cần giải phương trình đạo hàm bằng không để tìm ra các điểm dừng của hàm số. Các điểm dừng này là các ứng cử viên cho các điểm cực trị của hàm số.
Để xác định loại điểm dừng (điểm cực đại, điểm cực tiểu hoặc điểm uốn), chúng ta cần xét dấu đạo hàm cấp một trong các khoảng lân cận của điểm dừng. Nếu đạo hàm cấp một đổi dấu từ dương sang âm khi đi qua điểm dừng, thì đó là điểm cực đại. Ngược lại, nếu đạo hàm cấp một đổi dấu từ âm sang dương khi đi qua điểm dừng, thì đó là điểm cực tiểu.
Trong một số trường hợp, việc tính đạo hàm cấp hai có thể giúp chúng ta xác định loại điểm dừng một cách chính xác hơn. Đặc biệt, nếu đạo hàm cấp một bằng không tại một điểm dừng, chúng ta có thể sử dụng đạo hàm cấp hai để xác định xem điểm đó là điểm cực đại, điểm cực tiểu hay điểm uốn.
(Nội dung lời giải chi tiết bài 2.25 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính và kết quả cuối cùng. Lời giải sẽ được trình bày một cách rõ ràng, dễ hiểu và có kèm theo các giải thích chi tiết để giúp học sinh nắm vững kiến thức.)
Để giúp học sinh hiểu rõ hơn về cách giải bài tập về đạo hàm và ứng dụng của đạo hàm, chúng tôi sẽ cung cấp một số ví dụ minh họa và bài tập tương tự. Các ví dụ và bài tập này sẽ được giải chi tiết và có kèm theo các giải thích để giúp học sinh tự tin giải các bài tập tương tự.
Bài 2.25 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa mà chúng tôi cung cấp, các bạn học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy tiếp tục luyện tập và khám phá thêm nhiều bài tập toán thú vị khác tại giaitoan.edu.vn!