Bài 3.24 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay sau đây!
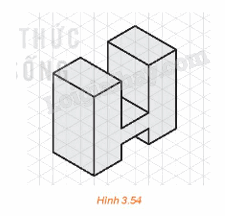
Một vật thể được biểu diễn trên giấy kẻ ô tam giác đều như trong Hình 3.54
Đề bài
Một vật thể được biểu diễn trên giấy kẻ ô tam giác đều như trong Hình 3.54. Quy ước chiều dài mỗi cạnh của tam giác đều là 10 mm, hãy lập bản vẽ kĩ thuật của vật thể đó và tính thể tích của nó.
Phương pháp giải - Xem chi tiết
Để lập bản vẽ kĩ thuật cho một vật thể ta thực hiện các bước sau:
- Quan sát vật thể, phân tích hình dạng và chọn các hướng chiếu vuông góc với các mặt của vật thể.
- Chọn tỉ lệ thích hợp với khổ giấy và kích thước vật thể. Bố trí ba hình chiếu cân đối trên bản vẽ theo các hình chữ nhật bao ngoài các hình chiếu.
- Vẽ ba hình chiếu từng phần của vật thể với các đường gióng tương ứng từ tổng quát đến chi tiết.
- Tô đậm các nét thấy của vật thể trên các hình chiếu, dùng nét đứt để biểu diễn các đường bao khuất.
- Kẻ các đường gióng kích thước, đường kích thước và ghi số kích thước trên các hình chiếu.
- Kẻ khung vẽ, khung tên, ghi các nội dung của khung tên.
Lời giải chi tiết
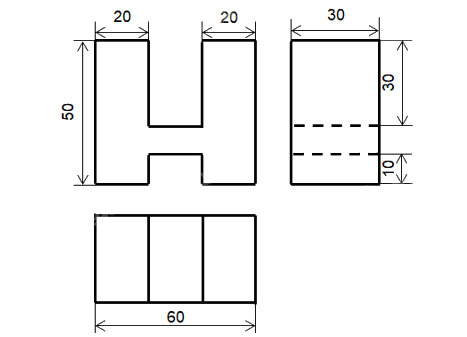
Bước 1: Nhận thấy rằng vật thể có dạng khối chữ H được bao bởi một hình hộp chữ nhật, hai phần rãnh cũng là hình hộp chữ nhật.
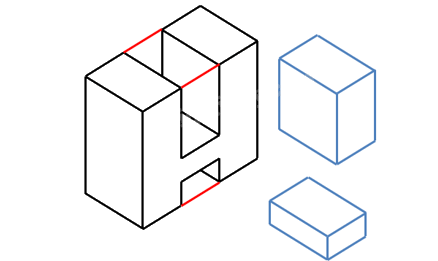
Bước 2: Chọn các hướng chiếu lần lượt vuông góc với mặt trước, mặt trên và mặt bên trái của vật thể.
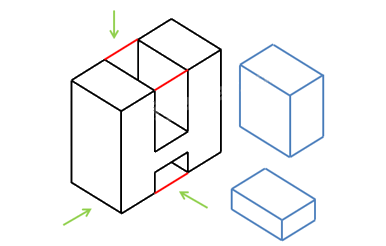
Bước 3: Lần lượt vẽ hình chiếu vuông góc của hình hộp chữ nhật bao bên ngoài vật thể, của khối chữ H và của rãnh hộp chữ nhật.

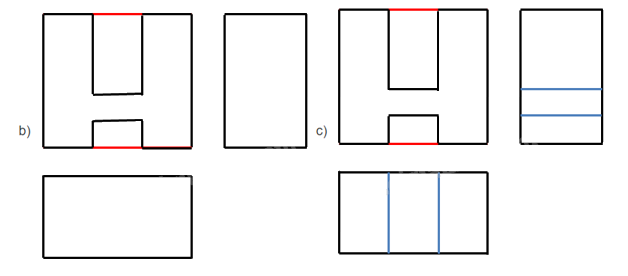
Bước 4: Xóa các nét thừa, chỉnh sửa các nét vẽ theo quy tắc: các đường thấy vẽ bằng nét liền; các đường khuất vẽ bằng nét đứt. Ghi các kích thước của vật thể trên các hình chiếu.
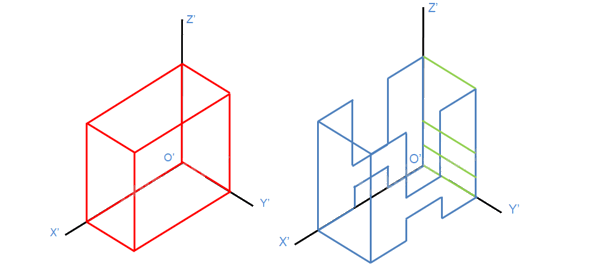
Bước 5: Vẽ hình chiếu trục đo vuông góc đều của vật thể.
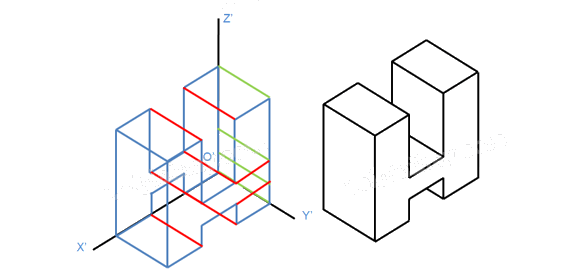
Bước 6: Hoàn thành khung tên, khung bản vẽ để được bản vẽ cuối cùng có dạng như sau:
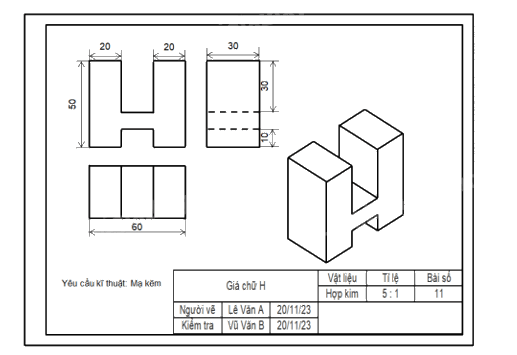
Ta có: Thể tích của giá chữ H bằng hiệu thể tích của hình hộp chữ nhật bao ngoài và thể tích của hai rãnh hộp chữ nhật.
Thể tích hình hộp chữ nhật bao ngoài là: 60 . 30 . 50 = 90 000 (mm3).
Thể tích rãnh hộp chữ nhật thứ nhất là: 30 . 20 . 30 = 18 000 (mm3).
Thể tích rãnh hộp chữ nhật thứ hai là: 20 . 30 . 10 = 6 000 (mm3).
Vậy thể tích của giá chữ H là: 90 000 – 18 000 – 6 000 = 66 000 (mm3).
Bài 3.24 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các bước giải bài toán cực trị.
Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Để tìm các điểm cực trị của hàm số y = f(x), ta thực hiện các bước sau:
Bước 1: Tính đạo hàm
f'(x) = 3x2 - 6x
Bước 2: Giải phương trình f'(x) = 0
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Khảo sát dấu của f'(x)
Ta xét các khoảng:
Bước 4: Kết luận
Dựa vào bảng xét dấu, ta thấy:
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Bài 3.24 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập điển hình về việc tìm cực trị của hàm số. Việc nắm vững phương pháp giải và các lưu ý quan trọng sẽ giúp bạn tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán.