Bài 2.27 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và giải quyết bài toán một cách hiệu quả.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.41.
Đề bài
Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.41.
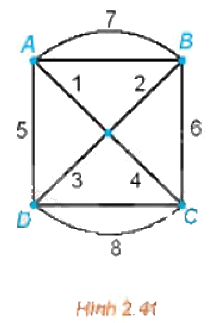
Phương pháp giải - Xem chi tiết
Dựa vào bài toán người đưa thư để làm
Lời giải chi tiết
Vì đồ thị Hình 2.41 là liên thông và các đỉnh đều có bậc chẵn (ở đây đều là bậc 4) nên đồ thị có chu trình Euler.
Một chu trình Euler xuất phát từ đỉnh A là ABCDABDCA và tổng độ dài của nó là
7 + 6 + 8 + 5 + 7 + 2 + 3 + 8 + 4 + 1 = 51.
Vậy một chu trình cần tìm là ABCDABDCA và có độ dài là 51.
Bài 2.27 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Giải cụ thể bài 2.27:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2 (ví dụ minh họa). Chúng ta sẽ áp dụng các bước trên để giải bài toán.
Bước 1: Tập xác định
Hàm số f(x) = x3 - 3x2 + 2 có tập xác định là D = ℝ (tập hợp tất cả các số thực).
Bước 2: Tính đạo hàm cấp nhất
f'(x) = 3x2 - 6x
Bước 3: Tìm các điểm dừng
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng.
Bước 4: Lập bảng biến thiên
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Xác định cực trị
Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại.
Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu.
Bước 6: Tính giá trị của hàm số tại các điểm cực trị
f(0) = 03 - 3(0)2 + 2 = 2 (giá trị cực đại)
f(2) = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2 (giá trị cực tiểu)
Kết luận:
Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Lưu ý:
Đây chỉ là một ví dụ minh họa. Bài 2.27 trang 51 Chuyên đề học tập Toán 11 Kết nối tri thức có thể có một hàm số khác. Bạn cần áp dụng các bước tương tự để giải bài toán cụ thể.
Việc hiểu rõ các khái niệm về đạo hàm, điểm dừng, khoảng đồng biến, nghịch biến và cực trị là rất quan trọng để giải quyết bài toán này. Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc các em học tập tốt!