Bài 1.7 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải, lý thuyết và bài tập Toán 11 Kết nối tri thức.
Cho hai đường tròn không đồng tâm, những có cùng bán kính (O1; R) và (O2; R).
Đề bài
Cho hai đường tròn không đồng tâm, những có cùng bán kính (O1; R) và (O2; R). Xác định phép đối xứng trục biến (O1; R) thành (O2; R).
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết
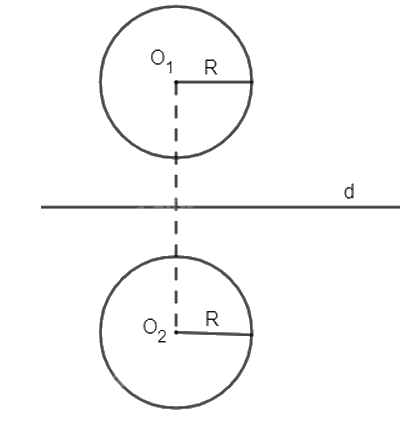
Phép đối xứng trục biến đường tròn thành đường tròn có cùng bán kính và có tâm là ảnh của tâm nên ta xác định phép đối xứng trục biến đường tròn (O1; R) thành đường tròn (O2; R) thì chỉ cần xác định phép đối xứng trục biến tâm O1 thành tâm O2.
Ta xác định đường trung trực d của đoạn thẳng O1O2. Khi đó phép đối xứng trục d biến O1 thành O2. Vậy phép đối xứng trục d biến đường tròn (O1; R) thành đường tròn (O2; R).
Bài 1.7 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về dãy số, cấp số cộng và cấp số nhân để giải quyết các bài toán thực tế. Để giải bài này, chúng ta cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ yêu cầu và tìm ra hướng giải phù hợp. Thông thường, bài tập về dãy số, cấp số cộng và cấp số nhân sẽ yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết của bài 1.7 trang 15, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)
Bài 1.7: Cho dãy số (un) với u1 = 2 và un+1 = 2un + 1. Tìm số hạng thứ 5 của dãy số.
Giải:
Vậy số hạng thứ 5 của dãy số là 47.
Để củng cố kiến thức và kỹ năng giải bài tập về dãy số, cấp số cộng và cấp số nhân, các em có thể tự giải các bài tập tương tự. Dưới đây là một số gợi ý:
Học toán online là một phương pháp học tập hiệu quả, nhưng đòi hỏi sự tự giác và kỷ luật. Để học tốt toán online, các em nên:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 1.7 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!