Bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài 1.15 này ngay bây giờ!
Bằng quan sát Hình 1.32, hãy chỉ ra một cách cắt hình đó thành ba phần giống nhau.
Đề bài
Bằng quan sát Hình 1.32, hãy chỉ ra một cách cắt hình đó thành ba phần giống nhau.

Phương pháp giải - Xem chi tiết
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
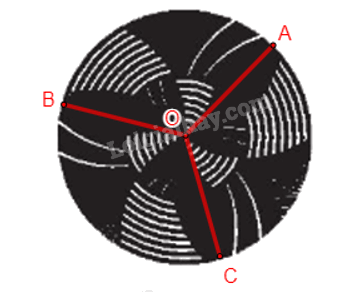
Ta có thể chia Hình 1.32 thành ba phần giống nhau bằng cách cắt theo đường màu đỏ như hình vẽ trên ( \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^o}\)).
Sử dụng phép quay \({Q_{\left( {O,{\rm{ }}120^\circ } \right)}}\;\)để thấy rõ các phần giống nhau của hình.
Bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến sự thay đổi của một đại lượng. Để giải bài này, chúng ta cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Đề bài thường yêu cầu chúng ta tìm đạo hàm của một hàm số, tìm cực trị của hàm số hoặc giải một phương trình liên quan đến đạo hàm. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
(Ở đây sẽ là lời giải chi tiết của bài 1.15, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh dễ dàng theo dõi và nắm bắt được kiến thức.)
Để giúp học sinh hiểu rõ hơn về cách giải bài 1.15, chúng ta sẽ đưa ra một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp học sinh rèn luyện kỹ năng và tự tin giải các bài tập khác.
Khi giải bài tập về đạo hàm, chúng ta cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
| Ứng dụng | Mô tả |
|---|---|
| Vật lý | Tính vận tốc, gia tốc của vật chuyển động. |
| Kinh tế | Tính chi phí biên, doanh thu biên. |
| Kỹ thuật | Tối ưu hóa thiết kế, điều khiển hệ thống. |
Bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa, các bạn học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự. Chúc các bạn học tập tốt!