Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 1.6 trang 15 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B.
Đề bài
Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B.
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết
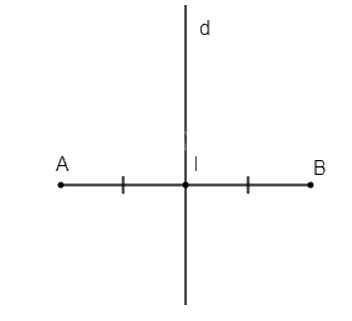
Cách xác định:
- Nối điểm A với điểm B;
- Xác định trung điểm I của AB. Qua I vẽ đường thẳng d vuông góc với AB.
Khi đó d là đường trung trực của đoạn thẳng AB.
Vậy ta có phép đối xứng trục d biến điểm A thành điểm B.
Bài 1.6 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các khái niệm về tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, cũng như cách vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu. Bài 1.6 thường yêu cầu học sinh:
Để giải bài 1.6 trang 15, chúng ta sẽ thực hiện theo các bước sau:
Ví dụ minh họa:
Giả sử hàm số được cho là y = x3 - 3x2 + 2. Chúng ta sẽ thực hiện các bước trên để giải bài 1.6.
Khi giải bài 1.6 trang 15, học sinh cần chú ý:
Bài 1.6 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức có ứng dụng thực tế trong nhiều lĩnh vực, chẳng hạn như:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.
Bài 1.6 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài toán quan trọng giúp học sinh hiểu sâu hơn về hàm số và đồ thị. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!