Bài 1.26 trang 31 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật lời giải mới nhất và chính xác nhất, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
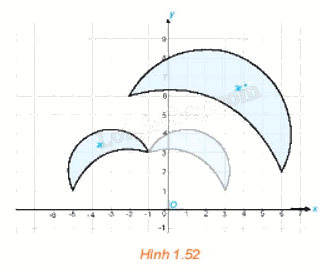
Hai hình ℋ và ℋ " trong Hình 1.52 được vẽ trên mặt phẳng tọa độ Oxy.
Đề bài
Hai hình ℋ và ℋ " trong Hình 1.52 được vẽ trên mặt phẳng tọa độ Oxy. Bằng quan sát, hãy chỉ ra một phép đối xứng trục f và một phép vị tự g sao cho phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép f và g (thực hiện f trước, g sau) biến hình ℋ thành hình ℋ ".
Phương pháp giải - Xem chi tiết
Quan sát hình 1.52 để làm
Lời giải chi tiết
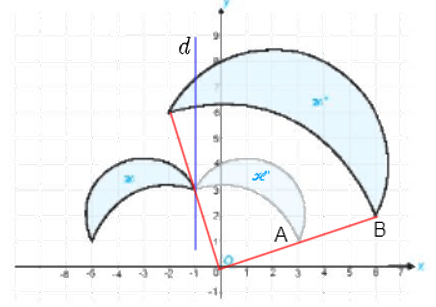
Quan sát Hình 1.52, ta thấy phép đối xứng trục d: x = – 1 biến hình ℋ thành hình ℋ '.
Ta thấy A(3; 1) thuộc hình ℋ ' và B(6; 2) thuộc hình ℋ ''.
Ta có \(\overrightarrow {OB} = \left( {6;\,2} \right)\) suy ra \(\overrightarrow {OB} = 2\overrightarrow {OA} \), khi đó phép vị tự tâm O, tỉ số 2 biến điểm A thành điểm B, thực hiện tương tự với các điểm khác, vậy ta có phép vị tự tâm O, tỉ số 2 biến hình ℋ ' thành hình ℋ ''.
Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng trục d có phương trình x = – 1 và phép vị tự \({V_{\left( {O,2} \right)}}\;\) (phép đối xứng trục trước, phép vị tự sau) biến hình ℋ thành hình ℋ ''.
Khi đó, phép đối xứng trục f là phép đối xứng trục d có phương trình x = – 1 và phép vị tự g là phép vị tự \({V_{\left( {O,2} \right)}}\;\)là các phép biến hình cần tìm.
Bài 1.26 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Để giải bài này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đạo hàm, đạo hàm của hàm số hợp, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Bài 1.26 thường yêu cầu học sinh thực hiện các bước sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể về bài 1.26. Giả sử hàm số cần khảo sát là: f(x) = x3 - 3x2 + 2.
f'(x) = 3x2 - 6x
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R (tập hợp tất cả các số thực).
Để tìm các điểm tới hạn, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm tới hạn.
Ta xét các khoảng sau:
Tại x = 0, f'(x) đổi dấu từ dương sang âm, do đó hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
Tại x = 2, f'(x) đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = 23 - 3(2)2 + 2 = -2.
Khi giải các bài tập về đạo hàm, học sinh cần chú ý các điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài 1.26 trang 31 Chuyên đề học tập Toán 11 Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!