Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 14, 15 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Chúng tôi cung cấp các bước giải bài tập một cách rõ ràng, logic, kèm theo các lưu ý quan trọng để các em hiểu sâu sắc về nội dung bài học.
Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a).
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.
Phương pháp giải:
- Lấy 2 điểm A, B thuộc d. Sau đó tìm ảnh của A, B qua phép đối xứng Ox là A’, B’. Ảnh của đường thẳng d chính là đường thẳng A’B’.
- Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Lời giải chi tiết:
Cách 1:
Lấy hai điểm A(0; – 1) và B(1; 2) thuộc d.
Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.
Khi đó A'(0; 1) và B'(1; – 2).
Vì d' là ảnh của đường thẳng d qua phép đối xứng trục Ox nên A' và B' thuộc d'.
Ta có: \(\overrightarrow {A'B'} = \left( {1;\, - 3} \right)\). Suy ra \(\overrightarrow {{n_{d'}}} = \left( {3;\,1} \right)\)
Vậy d' có phương trình là 3(x – 0) + (y – 1) = 0 hay 3x + y – 1 = 0.
Cách 2:
Gọi \(M'\left( {x';{\rm{ }}y'} \right)\) là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó \(x'{\rm{ }} = {\rm{ }}x\) và \(y'{\rm{ }} = {\rm{ }}-{\rm{ }}y.\)
Ta có: \(M\; \in \;d\; \Leftrightarrow \;3x-y-1 = 0\; \Leftrightarrow \;3x'-\left( {-y'} \right)-1 = 0\; \Leftrightarrow \;3x' + {\rm{ }}y'-1{\rm{ }} = 0\;\;\)
Vậy M' thuộc đường thẳng d' có phương trình là \(3x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0.\)
Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là \(\left( {{x_1};{\rm{ }}{y_1}} \right),\) N có tọa độ là \(\left( {{x_2};{\rm{ }}{y_2}} \right).\)
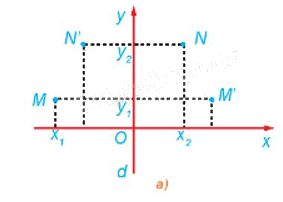
a) Hãy cho biết tọa độ của M', N'.
b) Tính \(M{N^2},{\rm{ }}M'N{'^2}\;\) theo tọa độ của các điểm tương ứng.
c) So sánh độ dài các đoạn thẳng MN, M'N'.
Phương pháp giải:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết:
a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).
Do đó \(M'\left( {-{\rm{ }}{x_1};{\rm{ }}{y_1}} \right)\) và \(N'\left( {-{\rm{ }}{x_2};{\rm{ }}{y_2}} \right).\)
b) Ta có:
\(\begin{array}{l}M{N^2} = {\left( {\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} } \right)^2} = {\rm{ }}{({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\\M'N{'^2} = {\left( {\sqrt {{{( - {x_2} - ( - {x_1}))}^2} + {{({y_2} - {y_1})}^2}} } \right)^2} = {\rm{ }}{-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}.\end{array}\)
c) Ta có: \({({x_2}\;-{\rm{ }}{x_1})^2}\; = {\rm{ }}{({x_1}\;-{\rm{ }}{x_2})^2}\; = {\rm{ }}{(-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}.\)
Do đó \({({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\; = {\rm{ }}{({\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\) hay \(M{N^2}\; = {\rm{ }}M'N{'^2}\)
Suy ra \(MN{\rm{ }} = {\rm{ }}M'N'.\)
Cho đường thẳng \(\Delta \) và hai điểm A, B, sao cho \(\Delta \) không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên \(\Delta \) (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.
Phương pháp giải:
Chứng minh M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Lời giải chi tiết:
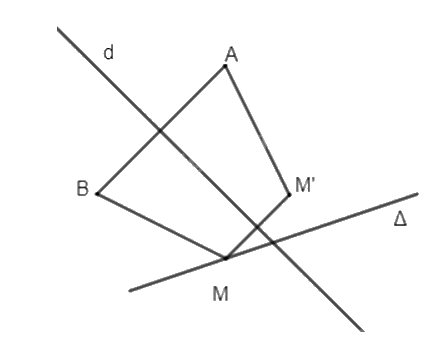
Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.
Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.
Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Vậy rằng M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
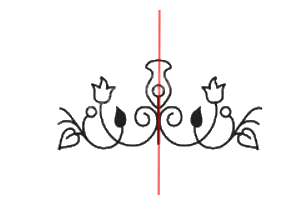
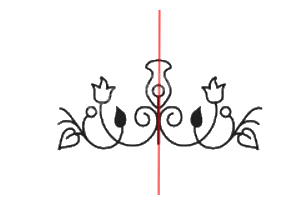
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.

Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
Quan sát hình ảnh ta thấy hình thứ hai từ trái sang có trục đối xứng.
Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là \(\left( {{x_1};{\rm{ }}{y_1}} \right),\) N có tọa độ là \(\left( {{x_2};{\rm{ }}{y_2}} \right).\)

a) Hãy cho biết tọa độ của M', N'.
b) Tính \(M{N^2},{\rm{ }}M'N{'^2}\;\) theo tọa độ của các điểm tương ứng.
c) So sánh độ dài các đoạn thẳng MN, M'N'.
Phương pháp giải:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết:
a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).
Do đó \(M'\left( {-{\rm{ }}{x_1};{\rm{ }}{y_1}} \right)\) và \(N'\left( {-{\rm{ }}{x_2};{\rm{ }}{y_2}} \right).\)
b) Ta có:
\(\begin{array}{l}M{N^2} = {\left( {\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} } \right)^2} = {\rm{ }}{({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\\M'N{'^2} = {\left( {\sqrt {{{( - {x_2} - ( - {x_1}))}^2} + {{({y_2} - {y_1})}^2}} } \right)^2} = {\rm{ }}{-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}.\end{array}\)
c) Ta có: \({({x_2}\;-{\rm{ }}{x_1})^2}\; = {\rm{ }}{({x_1}\;-{\rm{ }}{x_2})^2}\; = {\rm{ }}{(-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}.\)
Do đó \({({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\; = {\rm{ }}{({\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\) hay \(M{N^2}\; = {\rm{ }}M'N{'^2}\)
Suy ra \(MN{\rm{ }} = {\rm{ }}M'N'.\)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.
Phương pháp giải:
- Lấy 2 điểm A, B thuộc d. Sau đó tìm ảnh của A, B qua phép đối xứng Ox là A’, B’. Ảnh của đường thẳng d chính là đường thẳng A’B’.
- Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Lời giải chi tiết:
Cách 1:
Lấy hai điểm A(0; – 1) và B(1; 2) thuộc d.
Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.
Khi đó A'(0; 1) và B'(1; – 2).
Vì d' là ảnh của đường thẳng d qua phép đối xứng trục Ox nên A' và B' thuộc d'.
Ta có: \(\overrightarrow {A'B'} = \left( {1;\, - 3} \right)\). Suy ra \(\overrightarrow {{n_{d'}}} = \left( {3;\,1} \right)\)
Vậy d' có phương trình là 3(x – 0) + (y – 1) = 0 hay 3x + y – 1 = 0.
Cách 2:
Gọi \(M'\left( {x';{\rm{ }}y'} \right)\) là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó \(x'{\rm{ }} = {\rm{ }}x\) và \(y'{\rm{ }} = {\rm{ }}-{\rm{ }}y.\)
Ta có: \(M\; \in \;d\; \Leftrightarrow \;3x-y-1 = 0\; \Leftrightarrow \;3x'-\left( {-y'} \right)-1 = 0\; \Leftrightarrow \;3x' + {\rm{ }}y'-1{\rm{ }} = 0\;\;\)
Vậy M' thuộc đường thẳng d' có phương trình là \(3x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0.\)
Cho đường thẳng \(\Delta \) và hai điểm A, B, sao cho \(\Delta \) không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên \(\Delta \) (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.
Phương pháp giải:
Chứng minh M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Lời giải chi tiết:
Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.
Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.
Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Vậy rằng M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
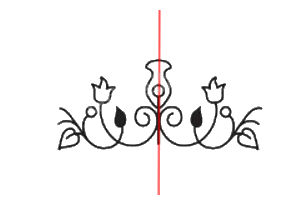
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.

Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
Quan sát hình ảnh ta thấy hình thứ hai từ trái sang có trục đối xứng.
Mục 2 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một phần kiến thức cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trong mục này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Để hiểu rõ hơn về nội dung của mục 2 trang 14, 15, chúng ta cần xem xét các khái niệm và định lý quan trọng được trình bày trong sách giáo khoa. Thông thường, mục này sẽ giới thiệu về một chủ đề mới hoặc mở rộng kiến thức đã học ở các chương trước. Các bài tập trong mục này thường được thiết kế để kiểm tra khả năng hiểu và vận dụng kiến thức của học sinh.
Dưới đây là hướng dẫn chi tiết giải các bài tập trong mục 2 trang 14, 15 Chuyên đề học tập Toán 11 - Kết nối tri thức:
Đề bài: (Nêu rõ đề bài)
Lời giải:
Đề bài: (Nêu rõ đề bài)
Lời giải:
Trong mục 2 trang 14, 15, học sinh có thể gặp các dạng bài tập sau:
Để giải bài tập trong mục 2 trang 14, 15 một cách hiệu quả, học sinh cần lưu ý những điều sau:
Việc giải bài tập là một phần không thể thiếu trong quá trình học tập môn Toán. Nó giúp học sinh củng cố kiến thức, rèn luyện kỹ năng và chuẩn bị cho các kỳ thi quan trọng. Đặc biệt, đối với học sinh lớp 11, việc nắm vững kiến thức Toán học là rất quan trọng để chuẩn bị cho kỳ thi THPT Quốc gia.
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách giáo khoa Toán 11. Chúng tôi hy vọng rằng, với sự hỗ trợ của Giaitoan.edu.vn, các em học sinh sẽ học tập môn Toán một cách hiệu quả và đạt kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| (Ví dụ công thức 1) | (Mô tả công thức 1) |
| (Ví dụ công thức 2) | (Mô tả công thức 2) |
Hy vọng bài viết này sẽ giúp các bạn học sinh giải quyết các bài tập trong mục 2 trang 14, 15 Chuyên đề học tập Toán 11 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc các bạn học tốt!