Bài 1.14 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và áp dụng linh hoạt vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 1.14 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (left( C right):{rm{ }}{left( {x{rm{ }}-{rm{ }}2} right)^2}; + {rm{ }}{y^2}; = {rm{ }}1.)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}1.\)
a) Tìm tọa độ tâm đường tròn (C') là ảnh của đường tròn (C) qua \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\).
b) Viết phương trình (C').
Phương pháp giải - Xem chi tiết
- Phép quay tâm O, góc quay \(\alpha\) :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
- Phương trình đường tròn tâm I(a;b), bán kính R là: \({\left( {x{\rm{ }}-{\rm{ a}}} \right)^2}\; + {\left( {{\rm{ }}y-{\rm{ b}}} \right)^2}\; = {\rm{ }}{R^2}.\)
Lời giải chi tiết
Ta có \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}1\). Suy ra đường tròn (C) có tâm I(2; 0) và bán kính R = 1.
Vì (C') là ảnh của đường tròn (C) qua phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) nên tâm I' của đường tròn (C') là ảnh của tâm I của đường tròn (C) qua phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\).
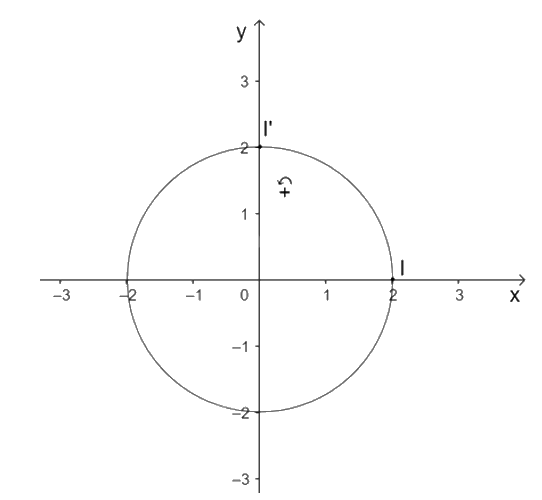
Vì I(2; 0) nên I'(0; 2).
b) Phép quay biến đường tròn thành đường tròn có cùng bán kính nên bán kính của đường tròn (C') là 1.
Vậy phương trình đường tròn (C') là \({x^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}2} \right)^2}\; = {\rm{ }}1.\)
Bài 1.14 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh tìm số hạng tổng quát của dãy số và chứng minh một số tính chất liên quan. Để giải bài tập này, chúng ta cần nắm vững các khái niệm về dãy số, cấp số cộng, cấp số nhân và các công thức tính số hạng tổng quát.
Đề bài yêu cầu tìm số hạng tổng quát của dãy số (un) được định nghĩa bởi công thức đệ quy u1 = 1 và un+1 = un + 2n + 1. Ngoài ra, cần chứng minh rằng un = n2.
Bước 1: Tìm số hạng tổng quát của dãy số
Ta có: u1 = 1
u2 = u1 + 2(1) + 1 = 1 + 2 + 1 = 4
u3 = u2 + 2(2) + 1 = 4 + 4 + 1 = 9
u4 = u3 + 2(3) + 1 = 9 + 6 + 1 = 16
Nhận thấy u1 = 12, u2 = 22, u3 = 32, u4 = 42. Do đó, ta dự đoán un = n2.
Bước 2: Chứng minh bằng phương pháp quy nạp
Bước cơ sở: Với n = 1, ta có u1 = 12 = 1, đúng với công thức.
Bước quy nạp: Giả sử công thức đúng với n = k, tức là uk = k2. Ta cần chứng minh công thức cũng đúng với n = k+1, tức là uk+1 = (k+1)2.
Ta có: uk+1 = uk + 2k + 1 = k2 + 2k + 1 = (k+1)2.
Vậy, công thức un = n2 đúng với mọi n ≥ 1.
Số hạng tổng quát của dãy số (un) là un = n2.
Các bài tập tương tự thường yêu cầu tìm số hạng tổng quát của dãy số được định nghĩa bằng công thức đệ quy. Phương pháp giải thường là:
Ngoài ra, có thể sử dụng các phương pháp khác như phương pháp lặp hoặc phương pháp giải phương trình đặc trưng để tìm số hạng tổng quát.
Dãy số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để nắm vững kiến thức về dãy số và rèn luyện kỹ năng giải bài tập, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác nhau với lời giải chi tiết, giúp các em học sinh tự tin hơn trong quá trình học tập.
Bài 1.14 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ về dãy số và phương pháp giải bài tập liên quan. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.