Giải bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 3.8 trang 65 trong Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

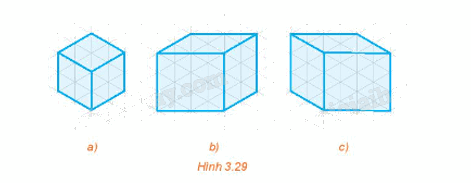
Trong các hình của Hình 3.29, hình nào là hình chiếu trục đo vuông góc đều của một hình lập phương? Giải thích vì sao.

Đề bài

Trong các hình của Hình 3.29, hình nào là hình chiếu trục đo vuông góc đều của một hình lập phương? Giải thích vì sao.

Giải bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Trong hình chiếu trục đo vuông góc đều có:

- Mặt phẳng chiếu (P) vuông góc với phương chiếu l;

- Các góc trục đo đều bằng 120^o.

- Các hệ số biến dạng đều bằng 1.

Lời giải chi tiết

Hình 3.29a là hình chiếu trục đo vuông góc đều của một hình lập phương vì đáy của hình chiếu vuông góc với phương chiếu l thẳng đứng; góc trục đo bằng 120°; hệ số biến dạng bằng 1 (chú ý đến độ dài các cạnh của hình chiếu).

Hình 3.29b và 3.29c không phải là hình chiếu trục đo vuông góc đều của hình lập phương vì góc trục đo không cùng bằng 120°; hệ số biến dạng không cùng bằng 1 (chú ý đến độ dài các cạnh của hình chiếu).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng toán học. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức: Tổng quan

Bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài toán 3.8 trang 65

Để giải quyết bài toán này, trước tiên chúng ta cần xác định rõ yêu cầu của đề bài. Thông thường, bài toán sẽ yêu cầu chúng ta:

Tính đạo hàm của hàm số đã cho.
Tìm các điểm cực trị của hàm số.
Xác định khoảng đồng biến và nghịch biến của hàm số.
Vẽ đồ thị hàm số.

Phương pháp giải bài toán 3.8 trang 65

Để giải bài toán 3.8 trang 65 một cách hiệu quả, chúng ta có thể áp dụng các phương pháp sau:

Sử dụng quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
Giải phương trình đạo hàm bằng 0: Để tìm các điểm cực trị, chúng ta cần giải phương trình f'(x) = 0.
Khảo sát dấu của đạo hàm: Dựa vào dấu của đạo hàm, chúng ta có thể xác định khoảng đồng biến và nghịch biến của hàm số.
Sử dụng đạo hàm cấp hai: Đạo hàm cấp hai có thể giúp chúng ta xác định tính chất lồi, lõm của đồ thị hàm số.

Ví dụ minh họa giải bài 3.8 trang 65

Giả sử bài toán 3.8 yêu cầu chúng ta giải hàm số f(x) = x³ - 3x² + 2. Chúng ta sẽ tiến hành giải như sau:

Tính đạo hàm: f'(x) = 3x² - 6x
Tìm điểm cực trị: Giải phương trình f'(x) = 0, ta được x = 0 và x = 2.
Khảo sát dấu của đạo hàm:
- Khi x < 0, f'(x) > 0, hàm số đồng biến.
- Khi 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
- Khi x > 2, f'(x) > 0, hàm số đồng biến.
Kết luận: Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

Lưu ý khi giải bài toán 3.8 trang 65

Khi giải bài toán 3.8 trang 65, bạn cần lưu ý những điều sau:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Nắm vững các khái niệm và quy tắc về đạo hàm.
Thực hiện các phép tính một cách cẩn thận và chính xác.
Kiểm tra lại kết quả để đảm bảo tính đúng đắn.

Ứng dụng của việc giải bài 3.8 trang 65

Việc giải bài 3.8 trang 65 không chỉ giúp bạn hiểu rõ hơn về đạo hàm mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như:

Kinh tế: Tìm điểm tối ưu trong sản xuất, kinh doanh.
Vật lý: Tính vận tốc, gia tốc của vật thể.
Kỹ thuật: Thiết kế các hệ thống tối ưu.

Tổng kết

Bài 3.8 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài toán quan trọng giúp bạn rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.