Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 2 trang 37, 38 của Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
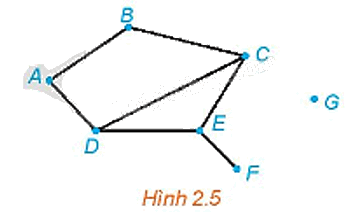
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó, ta có số đỉnh bậc 4 là: \(12{\rm{ }}-{\rm{ }}x.\)
Tổng số bậc của các đỉnh là: \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right).\)
Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là \(28{\rm{ }}.{\rm{ }}2{\rm{ }} = {\rm{ }}56.\)
Do đó, ta có phương trình \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right){\rm{ }} = {\rm{ }}56\), tức là \(8{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}0\). Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Phương pháp giải:
Dựa vào hình 2.5 để làm
Lời giải chi tiết:
Đỉnh là đầu mút của 0 cạnh là đỉnh G.
Đỉnh là đầu mút của 1 cạnh là đỉnh F.
Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.
Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.
Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó, ta có số đỉnh bậc 4 là: \(12{\rm{ }}-{\rm{ }}x.\)
Tổng số bậc của các đỉnh là: \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right).\)
Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là \(28{\rm{ }}.{\rm{ }}2{\rm{ }} = {\rm{ }}56.\)
Do đó, ta có phương trình \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right){\rm{ }} = {\rm{ }}56\), tức là \(8{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}0\). Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.
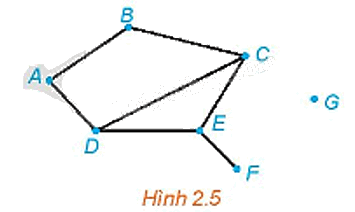
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Phương pháp giải:
Dựa vào hình 2.5 để làm
Lời giải chi tiết:
Đỉnh là đầu mút của 0 cạnh là đỉnh G.
Đỉnh là đầu mút của 1 cạnh là đỉnh F.
Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.
Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.
Mục 2 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc giải các bài tập trong mục này đòi hỏi học sinh phải nắm vững lý thuyết, hiểu rõ các định nghĩa, định lý và biết cách áp dụng chúng vào thực tế. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các phân tích, giải thích rõ ràng để giúp bạn hiểu sâu sắc hơn về kiến thức.
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập 1, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập 2, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập 3, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập 4, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Để giải tốt các bài tập trong mục 2, bạn cần nắm vững các kiến thức sau:
Để giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục 2, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: (Đưa ra một ví dụ cụ thể và giải chi tiết)
Để rèn luyện kỹ năng giải toán, bạn có thể thử giải các bài tập sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 37, 38 của Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc bạn học tập tốt!