Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 2.3 trang 40 thuộc Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải toán khoa học, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh của G
Đề bài
Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh của G và mọi cạnh của nó cũng là cạnh của G.
Những đồ thị nào trong các hình a), b), c) dưới đây là đồ thị con của đồ thị G?
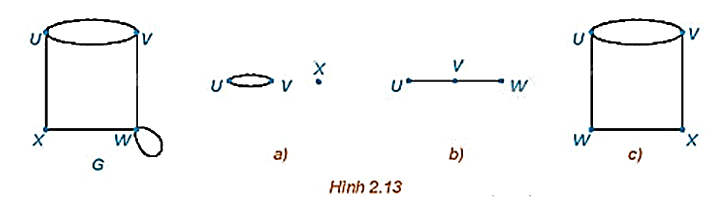
Phương pháp giải - Xem chi tiết
Một đồ thị G không liên thông đều được chia thành một số đồ thị (gọi là đồ thị con của G) liên thông, rời nhau, mỗi đồ thị con đó gọi là một thành phần liên thông của G.
Lời giải chi tiết
Các đồ thị a) và c) là đồ thị con của đồ thị G vì mọi đỉnh và mọi cạnh của từng đồ thị a) và c) đều là đỉnh và cạnh của G.
Đồ thị b) không phải là đồ thị con của đồ thị G vì đồ thị b) chứa cạnh UW không phải là cạnh của G.
Bài 2.3 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, đề bài sẽ yêu cầu chúng ta tìm đạo hàm của một hàm số, giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị, hoặc xét dấu đạo hàm để xác định khoảng đơn điệu của hàm số. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót.
Để giải bài 2.3 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta có thể áp dụng các bước sau:
Giả sử chúng ta có hàm số f(x) = x3 - 3x2 + 2. Để giải bài 2.3 trang 40, chúng ta thực hiện các bước sau:
| Khoảng | f'(x) | f(x) |
|---|---|---|
| (-∞; 0) | + | Đồng biến |
| (0; 2) | - | Nghịch biến |
| (2; +∞) | + | Đồng biến |
Khi giải bài 2.3 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức, bạn cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 2.3 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.