Bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kiến thức về các khái niệm đã học trong chuyên đề. Bài tập này thường yêu cầu học sinh vận dụng các công thức, định lý để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho phép tịnh tiến \({T_{\vec v}}\) và phép tịnh tiến \({T_{\vec v}}\).
Đề bài
Cho phép tịnh tiến \({T_{\vec v}}\) và phép tịnh tiến \({T_{\vec v}}\). Với điểm M bất kì, \({T_{\vec v}}\) biến M thành M’, \({T_{\vec v}}\) biến M’ thành M’’. Hỏi có phép tịnh tiến nào biến điểm M thành M’’ không?
Phương pháp giải - Xem chi tiết
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết
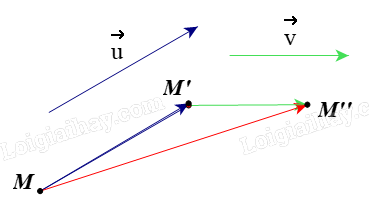
Theo đề, ta có \({T_{\vec u}}\left( M \right) = M'\), suy ra \(\overrightarrow {MM'} = \vec u\).
Ta lại có \({T_{\vec v}}\left( {M'} \right) = M''\), suy ra \(\overrightarrow {M'M''} = \vec v\).
Ta có \(\overrightarrow {MM''} = \overrightarrow {MM'} + \overrightarrow {M'M''} = \vec u + \vec v\)
Do đó \({T_{\vec u + \vec v}}\left( M \right) = M''\).
Vậy có phép tịnh tiến theo \(\vec u + \vec v\) biến điểm M thành điểm M’’.
Bài 1 trang 14 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc củng cố kiến thức về dãy số, cấp số cộng, cấp số nhân và ứng dụng của chúng trong các bài toán thực tế. Việc nắm vững các khái niệm này là nền tảng quan trọng cho việc học tập các kiến thức toán học nâng cao hơn ở các lớp trên.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta cần thực hiện các bước sau:
Ví dụ, giả sử bài 1 yêu cầu tìm số hạng thứ 10 của một cấp số cộng có số hạng đầu là 2 và công sai là 3. Chúng ta có thể sử dụng công thức tính số hạng tổng quát của cấp số cộng: un = u1 + (n-1)d. Thay u1 = 2, d = 3 và n = 10 vào công thức, ta được: u10 = 2 + (10-1)3 = 29. Vậy số hạng thứ 10 của cấp số cộng là 29.
Để giải các bài tập về dãy số một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tập về dãy số:
Bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về dãy số. Bằng cách nắm vững các công thức, luyện tập thường xuyên và sử dụng các tài liệu tham khảo, bạn có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.