Bài 5 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh phải vận dụng kiến thức đã học để tìm đạo hàm, xét dấu đạo hàm và xác định các điểm cực trị của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
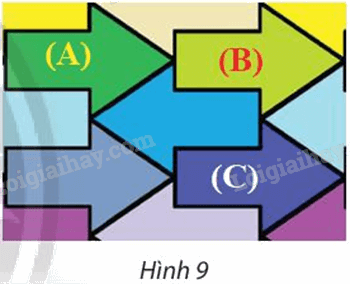
Trong Hình 9, tìm các vectơ \(\vec u\) và \(\vec v\) sao cho phép tịnh tiến \({T_{\vec u}}\)biến hình mũi tên (A) thành hình mũi tên (B) và phép tịnh tiến \({T_{\vec v}}\) biến hình mũi tên (A) thành hình mũi tên (C).
Đề bài
Trong Hình 9, tìm các vectơ \(\vec u\) và \(\vec v\) sao cho phép tịnh tiến \({T_{\vec u}}\)biến hình mũi tên (A) thành hình mũi tên (B) và phép tịnh tiến \({T_{\vec v}}\) biến hình mũi tên (A) thành hình mũi tên (C).
Phương pháp giải - Xem chi tiết
Quan sát hình 9 để làm
Lời giải chi tiết
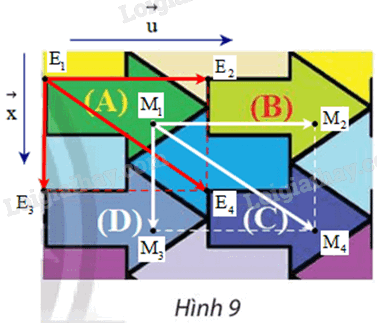
+ Gọi \({E_1}\) là một điểm trên hình mũi tên (A) và \(\vec u\) có phương song song với trục đối xứng của hình mũi tên (A), độ dài bằng độ dài từ điểm đầu tới điểm cuối của mũi tên (A) (hình vẽ).
Lấy điểm \({E_2}\;\) sao cho \(\overrightarrow {{E_1}{E_2}} = \vec u\)
Khi đó \({E_2}\;\) là một điểm trên hình mũi tên (B) có vị trí tương ứng với điểm \({E_1}\) trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm \({M_1}\) bất kì trên hình mũi tên (A), ta lấy điểm \({M_2}\) sao cho \(\overrightarrow {{M_1}{M_2}} = \vec u\) thì ta được tập hợp các điểm \({M_2}\) tạo thành hình mũi tên (B).
Do đó phép tịnh tiến theo \(\vec u\) biến hình mũi tên (A) thành hình mũi tên (B).
+ Ta gọi (D) là hình mũi tên nằm bên dưới hình mũi tên (A) và bên trái hình mũi tên (C) (như hình vẽ).
Gọi \({E_3}\) là một điểm trên hình mũi tên (D) có vị trí tương ứng với điểm E1 trên hình mũi tên (A).
Giả sử \(\vec x\) là vectơ có phương vuông góc với trục đối xứng của hình mũi tên (A), độ dài bằng độ dài từ điểm E1 đến điểm E3 (hình vẽ).
Tức là, \(\vec x = \overrightarrow {{E_1}{E_3}} \)
Lấy điểm \({E_4}\) sao cho tứ giác \({E_1}{E_2}{E_4}{E_3}\;\) là hình bình hành.
Áp dụng quy tắc hình bình hành, ta được \(\overrightarrow {{E_1}{E_4}} = \overrightarrow {{E_1}{E_2}} + \overrightarrow {{E_1}{E_3}} = \vec u + \vec x\).
Lúc này, ta thấy \({E_4}\) là một điểm trên hình mũi tên (C) có vị trí tương ứng với điểm \({E_1}\) trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm \({M_1}\) bất kì trên hình mũi tên (A), ta lấy điểm \({M_4}\) sao cho \(\overrightarrow {{M_1}{M_4}} = \vec u + \vec x\) thì ta được tập hợp các điểm M4 tạo thành hình mũi tên (C).
Do đó phép tịnh tiến theo \(\vec v = \vec u + \vec x\) biến hình mũi tên (A) thành hình mũi tên (C).
Bài 5 trang 14 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến khảo sát hàm số. Cụ thể, bài toán yêu cầu học sinh phân tích hàm số, tìm đạo hàm cấp một và cấp hai, xác định các điểm cực trị, và vẽ đồ thị hàm số. Việc nắm vững các bước giải bài toán này không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn trang bị cho họ những kỹ năng cần thiết để ứng dụng toán học vào cuộc sống.
Đề bài thường cho một hàm số cụ thể và yêu cầu học sinh thực hiện các bước sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử hàm số được cho là: f(x) = x3 - 3x2 + 2.
Hàm số f(x) = x3 - 3x2 + 2 là một đa thức, do đó tập xác định của hàm số là R (tập hợp tất cả các số thực).
f'(x) = 3x2 - 6x
f''(x) = 6x - 6
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
Xét dấu của f'(x) trên các khoảng:
Vậy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞).
Hàm số nghịch biến trên khoảng (0, 2).
Giải phương trình f''(x) = 0:
6x - 6 = 0
x = 1
Xét dấu của f''(x) trên các khoảng:
Vậy hàm số có điểm uốn tại x = 1.
Dựa vào các thông tin đã tìm được, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2.
Giải bài 5 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm. Bằng cách thực hiện các bước giải một cách cẩn thận và chính xác, học sinh có thể tự tin giải quyết các bài toán tương tự và nâng cao kỹ năng giải toán của mình.