Bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau.
Đề bài
Cho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau. Hãy chứng minh có hai phép vị tự biến đường tròn (I; R) thành đường tròn (I’; R’).
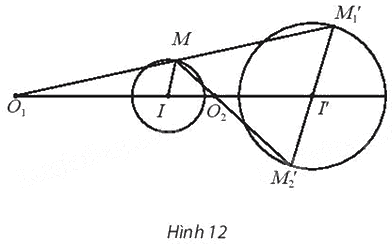
Phương pháp giải - Xem chi tiết
Quan sát hình 12, suy luận để chứng minh.
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Cần tìm được 2 giá trị của k thỏa mãn đề bài.
Lời giải chi tiết
Lấy điểm M bất kì thuộc \((I;{\rm{ }}R).\)
Đường thẳng qua I’ và song song với IM cắt đường tròn (I’; R’) tại hai điểm và (giả sử M, nằm cùng phía đối với đường thẳng II’ và M, nằm khác phía đối với đường thẳng II’).
Giả sử đường thẳng cắt đường thẳng II’ tại điểm O1 nằm ngoài đoạn OO’ và đường thẳng cắt đường thẳng II’ tại điểm O2 nằm trong đoạn II’.
Ta có biến đường tròn (I; R) thành đường tròn (I’; R’).
Suy ra \(R'{\rm{ }} = {\rm{ }}\left| k \right|.R.\)
Do đó \(|k| = \frac{{R'}}{R}\)
Mà \(k{\rm{ }} > {\rm{ }}0\) (do I, I’ nằm cùng phía đối với O1).
Suy ra \(k = \frac{{R'}}{R}\)
Ta có \({{\rm{V}}_{\left( {{{\rm{O}}_2},{\rm{k'}}} \right)}}\) biến đường tròn \(\left( {I;{\rm{ }}R} \right)\) thành đường tròn \(\left( {I';{\rm{ }}R'} \right).\)
Chứng minh tương tự, ta được khi I, I’ nằm khác phía đối với O2, ta có \(k' = - \frac{{R'}}{R}\)
Vậy ta có hai phép vị tự thỏa mãn yêu cầu bài toán là \({V_{\left( {{O_1},\frac{{R'}}{R}} \right)}}\) và \({V_{\left( {{O_2}, - \frac{{R'}}{R}} \right)}}\).
Bài 5 trang 36 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định và tính toán đạo hàm của hàm số, sau đó sử dụng đạo hàm để tìm ra các giá trị cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết bài toán này một cách hiệu quả.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Đề bài thường cung cấp một hàm số cụ thể và yêu cầu chúng ta thực hiện một hoặc nhiều thao tác như:
Để giải quyết bài toán này, chúng ta cần áp dụng các công thức và quy tắc đạo hàm đã học, kết hợp với việc phân tích và suy luận logic. Ngoài ra, việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị có thể giúp chúng ta kiểm tra lại kết quả và trực quan hóa bài toán.
(Giả sử đề bài cụ thể là: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm các điểm cực trị của hàm số.)
y' = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của đạo hàm cấp hai (y''):
y'' = 6x - 6
Tại x = 0, y'' = -6 < 0, vậy hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
Tại x = 2, y'' = 6 > 0, vậy hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.
Kết luận: Hàm số y = x3 - 3x2 + 2 đạt cực đại tại điểm (0, 2) và đạt cực tiểu tại điểm (2, -2).
Ngoài bài toán tìm điểm cực trị, bài 5 trang 36 và các bài tập tương tự còn có thể yêu cầu chúng ta:
Để giải quyết các bài toán này, chúng ta cần nắm vững các kiến thức về đạo hàm, khoảng đồng biến, nghịch biến, điểm uốn và cách vẽ đồ thị hàm số. Ngoài ra, việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp chúng ta rèn luyện kỹ năng và tư duy giải quyết vấn đề.
Khi giải bài tập về đạo hàm, chúng ta cần lưu ý một số điểm sau:
Bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.