Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 59, 60, 61 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp các em hiểu sâu sắc bản chất của từng bài toán.
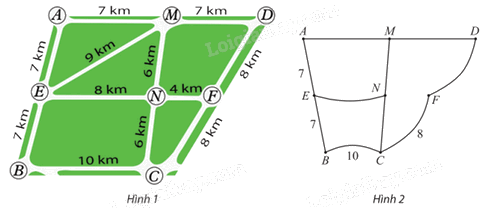
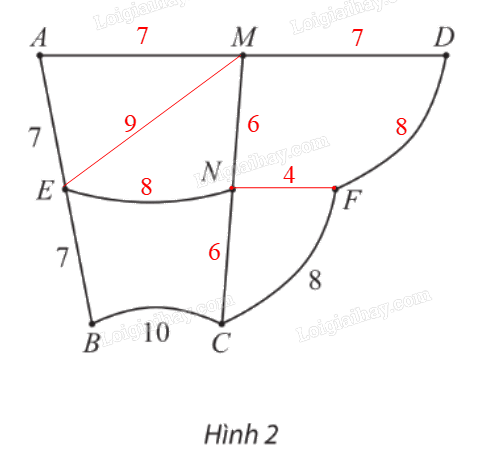
Để biểu diễn các con đường nối các giao lộ cùng với độ dài của chúng như sơ đồ ở Hình 1, một học sinh đã vẽ đồ thị như Hình 2.
Để biểu diễn các con đường nối các giao lộ cùng với độ dài của chúng như sơ đồ ở Hình 1, một học sinh đã vẽ đồ thị như Hình 2. Chỉ ra các cạnh và số biểu diễn độ dài con đường còn thiếu trong Hình 2.
Phương pháp giải:
Quan sát hình vè để trả lời
Lời giải chi tiết:
Các cạnh còn thiếu trong Hình 2 là: EM, NF.
Các số biểu diễn độ dài con đường còn thiếu trong Hình 2 là:
⦁ 7 (biểu diễn độ dài AM, MD);
⦁ 9 (biểu diễn độ dài EM);
⦁ 6 (biểu diễn độ dài MN, CN);
⦁ 8 (biểu diễn độ dài DF, EN);
⦁ 4 (biểu diễn độ dài NF).
Đồ thị biểu diễn đầy đủ các thông tin trong Hình 1 là:
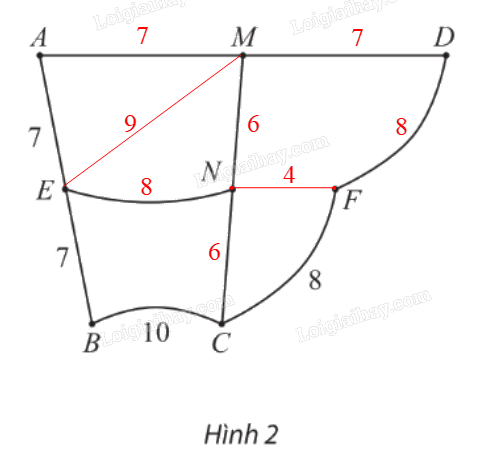
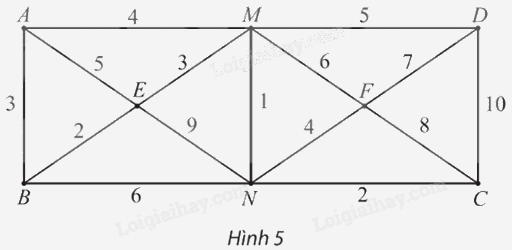
Cho đồ thị có trọng số như Hình 5.
a) Chỉ ra trọng số của các cạnh AE, MN, CN.
b) Tính độ dài của các đường đi ABEN, EMFNE.
c) Chỉ ra ba đường đi khác nhau từ A đến D và tính độ dài của chúng.
d) Đường đi EMF có phải là đường đi ngắn nhất từ E đến F không?
Phương pháp giải:
Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh, chi phí vận chuyển trên mỗi cạnh đó,…) thì đồ thị G được gọi là đồ thị có trọng số. Trọng số của cạnh a kí hiệu là \({w_a}\).
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B.
Lời giải chi tiết:
a) Ta có \({w_{AE}}\; = {\rm{ }}5;{\rm{ }}{w_{MN}}\; = {\rm{ }}1;{\rm{ }}{w_{CN}}\; = {\rm{ }}2.\)
b) Ta có:
\({l_{ABEN}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BE}}\; + {\rm{ }}{w_{EN}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}14;\)
\({l_{EMFNE}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MF}}\; + {\rm{ }}{w_{FN}}\; + {\rm{ }}{w_{NE}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}22.\)
c) Ba đường đi khác nhau từ A đến D là: AMD, AENFD, ABNCD.
Ta có:
\({l_{AMD}}\; = {\rm{ }}{w_{AM}}\; + {\rm{ }}{w_{MD}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}9.\)
\({l_{AENFD}}\; = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EN}}\; + {\rm{ }}{w_{NF}}\; + {\rm{ }}{w_{FD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}25.\)
\({l_{ABNCD}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BN}}\; + {\rm{ }}{w_{NC}}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}10{\rm{ }} = {\rm{ }}21.\)
Vậy ba đường đi khác nhau từ A đến D là AMD (có độ dài bằng 9), AENFD (có độ dài bằng 25), ABNCD (có độ dài bằng 21).
d) Ta có EMNF là một đường đi từ E đến F.
Mà \({l_{EMNF}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MN}}\; + {\rm{ }}{w_{NF}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}1{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}8,{\rm{ }}{l_{EMF}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MF}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}9.\)
Vì 8 < 9 nên \({l_{EMNF}}\; < {\rm{ }}{l_{EMF}}.\)
Vậy đường đi EMF không phải là đường đi ngắn nhất từ E đến F.
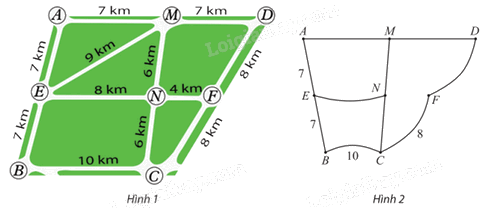
Để biểu diễn các con đường nối các giao lộ cùng với độ dài của chúng như sơ đồ ở Hình 1, một học sinh đã vẽ đồ thị như Hình 2. Chỉ ra các cạnh và số biểu diễn độ dài con đường còn thiếu trong Hình 2.
Phương pháp giải:
Quan sát hình vè để trả lời
Lời giải chi tiết:
Các cạnh còn thiếu trong Hình 2 là: EM, NF.
Các số biểu diễn độ dài con đường còn thiếu trong Hình 2 là:
⦁ 7 (biểu diễn độ dài AM, MD);
⦁ 9 (biểu diễn độ dài EM);
⦁ 6 (biểu diễn độ dài MN, CN);
⦁ 8 (biểu diễn độ dài DF, EN);
⦁ 4 (biểu diễn độ dài NF).
Đồ thị biểu diễn đầy đủ các thông tin trong Hình 1 là:
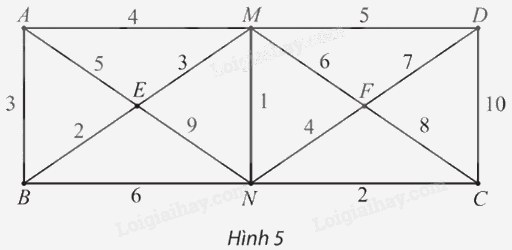
Cho đồ thị có trọng số như Hình 5.
a) Chỉ ra trọng số của các cạnh AE, MN, CN.
b) Tính độ dài của các đường đi ABEN, EMFNE.
c) Chỉ ra ba đường đi khác nhau từ A đến D và tính độ dài của chúng.
d) Đường đi EMF có phải là đường đi ngắn nhất từ E đến F không?
Phương pháp giải:
Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh, chi phí vận chuyển trên mỗi cạnh đó,…) thì đồ thị G được gọi là đồ thị có trọng số. Trọng số của cạnh a kí hiệu là \({w_a}\).
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B.
Lời giải chi tiết:
a) Ta có \({w_{AE}}\; = {\rm{ }}5;{\rm{ }}{w_{MN}}\; = {\rm{ }}1;{\rm{ }}{w_{CN}}\; = {\rm{ }}2.\)
b) Ta có:
\({l_{ABEN}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BE}}\; + {\rm{ }}{w_{EN}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}14;\)
\({l_{EMFNE}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MF}}\; + {\rm{ }}{w_{FN}}\; + {\rm{ }}{w_{NE}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}22.\)
c) Ba đường đi khác nhau từ A đến D là: AMD, AENFD, ABNCD.
Ta có:
\({l_{AMD}}\; = {\rm{ }}{w_{AM}}\; + {\rm{ }}{w_{MD}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}9.\)
\({l_{AENFD}}\; = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EN}}\; + {\rm{ }}{w_{NF}}\; + {\rm{ }}{w_{FD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}25.\)
\({l_{ABNCD}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BN}}\; + {\rm{ }}{w_{NC}}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}10{\rm{ }} = {\rm{ }}21.\)
Vậy ba đường đi khác nhau từ A đến D là AMD (có độ dài bằng 9), AENFD (có độ dài bằng 25), ABNCD (có độ dài bằng 21).
d) Ta có EMNF là một đường đi từ E đến F.
Mà \({l_{EMNF}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MN}}\; + {\rm{ }}{w_{NF}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}1{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}8,{\rm{ }}{l_{EMF}}\; = {\rm{ }}{w_{EM}}\; + {\rm{ }}{w_{MF}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}9.\)
Vì 8 < 9 nên \({l_{EMNF}}\; < {\rm{ }}{l_{EMF}}.\)
Vậy đường đi EMF không phải là đường đi ngắn nhất từ E đến F.
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng phân tích.
Trang 59 thường chứa các bài tập vận dụng kiến thức cơ bản của mục học. Các bài tập này thường có dạng trắc nghiệm hoặc tự luận đơn giản, yêu cầu học sinh thực hiện các phép tính, biến đổi đại số hoặc chứng minh các đẳng thức. Để giải tốt các bài tập này, học sinh cần:
Trang 60 thường chứa các bài tập vận dụng kiến thức đã học vào giải quyết các bài toán thực tế hoặc các bài toán có tính chất mở rộng. Các bài tập này đòi hỏi học sinh phải có khả năng tư duy sáng tạo, liên hệ kiến thức với thực tế và áp dụng các phương pháp giải khác nhau. Để giải tốt các bài tập này, học sinh cần:
Trang 61 thường chứa các bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng khác nhau. Các bài tập này đòi hỏi học sinh phải có khả năng tổng hợp, phân tích và đánh giá thông tin. Để giải tốt các bài tập này, học sinh cần:
Để học tốt môn Toán, đặc biệt là các chuyên đề học tập, học sinh cần:
Ngoài sách giáo khoa và sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập mục 1 trang 59, 60, 61 Chuyên đề học tập Toán 11 - Chân trời sáng tạo là một bước quan trọng trong quá trình học tập môn Toán của các em. Hy vọng rằng với lời giải chi tiết và các hướng dẫn hữu ích trên đây, các em sẽ tự tin hơn trong việc giải quyết các bài toán và đạt kết quả tốt trong môn học.