Chào mừng các em học sinh đến với lời giải chi tiết bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Gọi O được gọi là tâm đối xứng quay bậc (n{rm{ }}(n in mathbb{N}*)) của hình ℋ nếu sau khi thực hiện phép quay ({Q_{left( {O,frac{{360^circ }}{n}} right)}})
Đề bài
Gọi O được gọi là tâm đối xứng quay bậc \(n{\rm{ }}(n \in \mathbb{N}*)\) của hình ℋ nếu sau khi thực hiện phép quay \({Q_{\left( {O,\frac{{360^\circ }}{n}} \right)}}\) ta lại được chính hình ℋ. Hình có tâm đối xứng quay bậc n gọi là hình đối xứng quay bậc n. Tìm các hình đối xứng quay trong Hình 2.
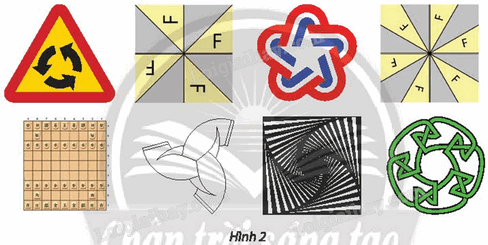
Phương pháp giải - Xem chi tiết
Quan sát hình 2, suy luận để trả lời
Lời giải chi tiết
Ta đặt tên cho các hình vẽ trong Hình 2 theo thứ tự từ trái qua phải, từ trên xuống dưới là: a, b, c, d, e, f, g, h.
⦁ Xét Hình 2a: biển báo có dạng hình tam giác đều.

Gọi O là tâm đường tròn ngoại tiếp tam giác, điểm A là một đỉnh của tam giác.
Phép quay tâm O, góc quay 120° biến điểm A thành điểm A’.
Khi đó ta thấy điểm A’ nằm trên Hình 2a ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2a.
Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2a ban đầu.
Vì vậy phép quay biến Hình 2a thành chính nó là phép quay tâm O, góc quay 120°.
Ta có \(\frac{{360^\circ }}{n} = 120^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}3 \in \mathbb{N}*.\)
Vì vậy Hình 2a có tâm đối xứng quay bậc 3.
⦁ Xét Hình 2b: có dạng hình vuông.
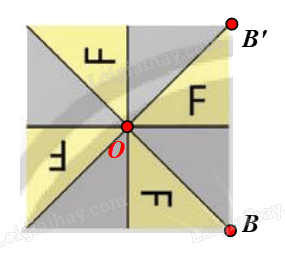
Gọi O là tâm hình vuông và B là một đỉnh của hình vuông.
Phép quay tâm O, góc quay 90° biến điểm B thành điểm B’.
Khi đó ta thấy điểm B’ nằm trên Hình 2b ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2b.
Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2b ban đầu.
Vì vậy phép quay biến Hình 2b thành chính nó là phép quay tâm O, góc quay 90°.
Ta có \(\frac{{360^\circ }}{n} = 90^\circ \) Suy ra \(n{\rm{ }} = {\rm{ }}4 \in \mathbb{N}*.\)
Vì vậy Hình 2b có tâm đối xứng quay bậc 4.
⦁ Xét Hình 2c:

Chọn hai điểm O, C như hình vẽ.
Phép quay tâm O, góc quay 72° biến điểm C thành điểm C’.
Khi đó ta thấy điểm C’ nằm trên Hình 2c ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2c.
Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2c ban đầu.
Vì vậy phép quay biến Hình 2c thành chính nó là phép quay tâm O, góc quay 72°.
Ta có \(\frac{{360^\circ }}{n} = 72^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}5 \in \mathbb{N}*.\)
Vì vậy Hình 2c có tâm đối xứng quay bậc 5.
⦁ Xét Hình 2d: có dạng hình vuông
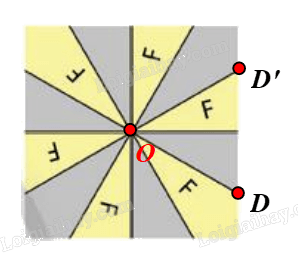
Gọi O là tâm hình vuông. Chọn điểm D như hình vẽ.
Phép quay tâm O, góc quay 60° biến điểm D thành điểm D’.
Khi đó ta thấy điểm D’ nằm trên Hình 2d ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2d.
Khi đó qua phép quay tâm O, góc quay 60°, ta cũng xác định được ảnh của các điểm đó trên Hình 2d ban đầu.
Vì vậy phép quay biến Hình 2d thành chính nó là phép quay tâm O, góc quay 60°.
Ta có \(\frac{{360^\circ }}{n} = 60^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}6 \in \mathbb{N}*.\)
Vì vậy Hình 2d có tâm đối xứng quay bậc 6.
⦁ Xét Hình 2e: có dạng hình vuông.
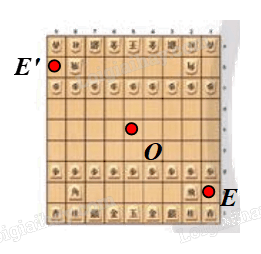
Gọi O là tâm hình vuông. Chọn điểm E như hình vẽ.
Phép quay tâm O, góc quay 180° biến điểm E thành điểm E’.
Khi đó ta thấy điểm E’ nằm trên Hình 2e ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2e.
Khi đó qua phép quay tâm O, góc quay 180°, ta cũng xác định được ảnh của các điểm đó trên Hình 2e ban đầu.
Vì vậy phép quay biến Hình 2e thành chính nó là phép quay tâm O, góc quay 180°.
Ta có \(\frac{{360^\circ }}{n} = 180^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}2 \in \mathbb{N}*.\)
Vì vậy Hình 2e có tâm đối xứng quay bậc 2.
⦁ Xét Hình 2f:
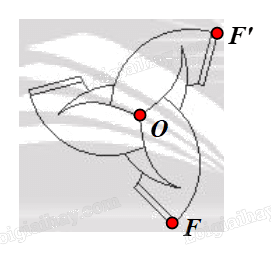
Chọn hai điểm O, F như hình vẽ.
Phép quay tâm O, góc quay 120° biến điểm F thành điểm F’.
Khi đó ta thấy điểm F’ nằm trên Hình 2f ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2f.
Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2f ban đầu.
Vì vậy phép quay biến Hình 2f thành chính nó là phép quay tâm O, góc quay 120°.
Ta có \(\frac{{360^\circ }}{n} = 120^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}3 \in \mathbb{N}*.\)
Vì vậy Hình 2f có tâm đối xứng quay bậc 3.
⦁ Xét Hình 2g: có dạng hình vuông.
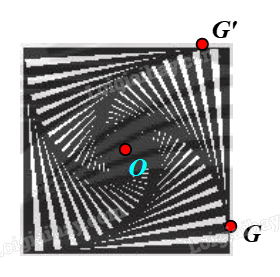
Gọi O là tâm hình vuông. Chọn điểm G như hình vẽ.
Phép quay tâm O, góc quay 90° biến điểm G thành điểm G’.
Khi đó ta thấy điểm G’ nằm trên Hình 2g ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2g.
Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2g ban đầu.
Vì vậy phép quay biến Hình 2g thành chính nó là phép quay tâm O, góc quay 90°.
Ta có \(\frac{{360^\circ }}{n} = 90^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}4 \in \mathbb{N}*.\)
Vì vậy Hình 2g có tâm đối xứng quay bậc 4.
⦁ Xét Hình 2h: có dạng hình tròn
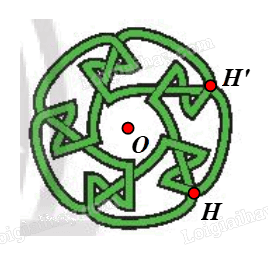
Gọi O là tâm hình tròn. Chọn điểm H như hình vẽ.
Phép quay tâm O, góc quay 72° biến điểm H thành điểm H’.
Khi đó ta thấy điểm H’ nằm trên Hình 2h ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2h.
Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2h ban đầu.
Vì vậy phép quay biến Hình 2h thành chính nó là phép quay tâm O, góc quay 72°.
Ta có \(\frac{{360^\circ }}{n} = 72^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}5 \in \mathbb{N}*.\)
Vì vậy Hình 2h có tâm đối xứng quay bậc 5.
Vậy tất cả các hình trong Hình 2 đều là hình đối xứng quay có bậc lần lượt là 3; 4; 5; 6; 2; 3; 4; 5 (tính thứ tự các hình từ trái qua phải và từ trên xuống dưới).
Bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 16 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 16, chúng ta sẽ đi vào giải chi tiết từng bài tập.
Ví dụ: Tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1.
Lời giải:
y' = 3x2 - 4x + 5
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
Ví dụ: Khảo sát sự biến thiên của hàm số y = x4 - 4x2 + 3.
Lời giải:
Để khảo sát sự biến thiên của hàm số, ta thực hiện các bước sau:
Ví dụ: Tìm giá trị lớn nhất của hàm số y = -x2 + 4x + 1 trên đoạn [-1; 3].
Lời giải:
Để tìm giá trị lớn nhất của hàm số trên đoạn [-1; 3], ta thực hiện các bước sau:
Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ hiểu rõ hơn về cách giải bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc các em học tập tốt!