Bài 2 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chuyên đề. Bài tập này thường yêu cầu vận dụng các công thức, định lý và phương pháp giải toán đã được trình bày trong sách giáo khoa.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh có thể tự học và ôn tập hiệu quả.
Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là
Đề bài
Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là
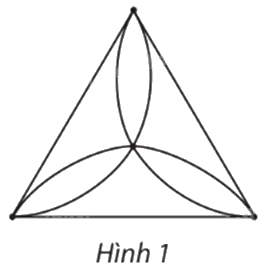
A. 20.
B. 18.
C. 12.
D. 9.
Phương pháp giải - Xem chi tiết
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết
Đáp án đúng là: B

Gọi các đỉnh của đồ thị ở Hình 1 là: A, B, C, D (hình vẽ).
Ta có \(d\left( A \right){\rm{ }} = {\rm{ }}d\left( B \right){\rm{ }} = {\rm{ }}d\left( C \right){\rm{ }} = {\rm{ }}4,{\rm{ }}d\left( D \right){\rm{ }} = {\rm{ }}6.\)
Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là: \(4{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}18.\)
Vậy ta chọn phương án B.
Bài 2 trang 67 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo thường tập trung vào việc vận dụng kiến thức về dãy số, cấp số cộng, cấp số nhân, hoặc các chủ đề khác tùy thuộc vào nội dung chuyên đề. Mục tiêu chính của bài tập là giúp học sinh củng cố lý thuyết và rèn luyện kỹ năng giải toán thực tế.
Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Sau đó, cần lựa chọn phương pháp giải phù hợp, có thể là sử dụng công thức, định lý, hoặc các kỹ thuật biến đổi đại số. Việc phân tích đề bài một cách cẩn thận sẽ giúp học sinh tránh được những sai sót không đáng có.
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 2 trang 67. Giả sử bài tập yêu cầu tính tổng của một cấp số cộng, lời giải sẽ bao gồm các bước sau:
Giả sử bài 2 yêu cầu tính tổng của cấp số cộng có số hạng đầu u1 = 2, công sai d = 3 và có 10 số hạng. Khi đó:
Vậy tổng của cấp số cộng là 155.
Ngoài bài 2 trang 67, Chuyên đề học tập Toán 11 Chân trời sáng tạo còn có nhiều bài tập tương tự về dãy số, cấp số cộng, cấp số nhân. Để giải các bài tập này, học sinh cần nắm vững các công thức và định lý liên quan, đồng thời rèn luyện kỹ năng giải toán thường xuyên.
Kiến thức về dãy số, cấp số cộng, cấp số nhân có ứng dụng rộng rãi trong thực tế, chẳng hạn như trong lĩnh vực tài chính, kinh tế, vật lý, và kỹ thuật. Việc nắm vững kiến thức này sẽ giúp học sinh có thể giải quyết các vấn đề thực tế một cách hiệu quả.
Bài 2 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Bằng cách phân tích đề bài, lựa chọn phương pháp giải phù hợp và kiểm tra lại kết quả, học sinh có thể tự tin giải quyết bài tập một cách chính xác và hiệu quả. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh học tập tốt hơn.
| Công thức | Mô tả |
|---|---|
| Số hạng tổng quát của cấp số cộng | un = u1 + (n-1)d |
| Tổng của n số hạng đầu của cấp số cộng | Sn = n/2 * (u1 + un) hoặc Sn = n/2 * (2u1 + (n-1)d) |
| Số hạng tổng quát của cấp số nhân | un = u1 * q^(n-1) |
| Tổng của n số hạng đầu của cấp số nhân | Sn = u1 * (1 - q^n) / (1 - q) (với q ≠ 1) |