Bài 5 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chương trình. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin giải quyết bài tập và nắm vững kiến thức Toán 11.
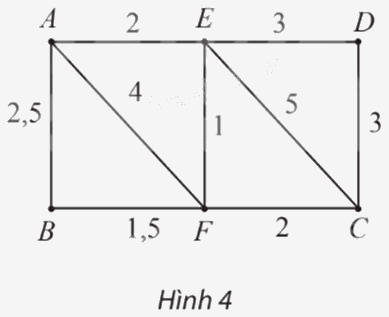
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là
Đề bài
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là
A. AEC.
B. AEFC.
C. AC.
D. AFC.
Phương pháp giải - Xem chi tiết
Thuật toán tìm đường đi ngắn nhất từ đỉnh A đến đỉnh T
Mở đầu: Gán nhãn của A bằng 0, các đỉnh khác bằng\(\infty \). Khoanh tròn đỉnh A.
Các bước lặp
Trong mỗi bước lặp thực hiện các thao tác sau đây:
- Gọi U là đỉnh vừa được khoanh tròn ở bước trước. Trong các đỉnh chưa khoanh tròn, xét lần lượt từng đỉnh V kề với đỉnh U, tính \({n_U}\; + {\rm{ }}{w_{UV}}\), rồi so sánh số này với nhãn hiện tại \({n_V}\;\) của V. Nếu số đó nhỏ hơn thì đổi nhãn \({n_V}\;\) bằng số đó.
- So sánh nhãn của tất cả các đỉnh chưa khoanh tròn. Đỉnh nào có nhãn nhỏ nhất thì khoanh tròn đỉnh đó (nếu có nhiều đỉnh hư vậy thì khoanh một đỉnh tùy ý trong số đó).
- Nếu đỉnh T chưa được khoanh tròn thì thực hiện bước lặp tiếp theo, trái lại thì kết thức các bước lặp.
Kết luận: Dò lại các bước lặp để viết được nhãn \({n_T}\) của T dưới dạng tổng độ dài các cạnh. Từ đó nhận được đường đi ngắn nhất từ A đến T cùng với độ dài của nó.
Lời giải chi tiết
Đáp án đúng là: B
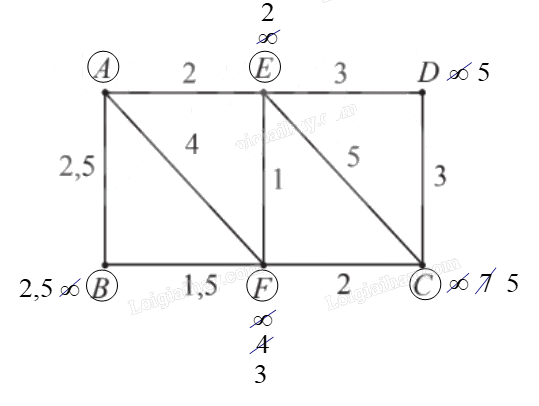
– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm E, F, B, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}2\).Vì \(2{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 2.
⦁ \({n_F}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AF}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}4\).Vì \(4{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 4.
⦁ \({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2,5{\rm{ }} = {\rm{ }}2,5\).Vì \(2,5{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 2,5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, C, F, ta có:
⦁ \({n_D}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{ED}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 5.
⦁ \({n_C}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EC}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}7\).Vì \(7{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 7.
⦁ \({n_F}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}4\) (4 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B chỉ có F, ta có:
\({n_F}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BF}}\; = {\rm{ }}2,5{\rm{ }} + {\rm{ }}1,5{\rm{ }} = {\rm{ }}4\).Vì \(4{\rm{ }} > {\rm{ }}3\) (3 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ có C, ta có:
\({n_C}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}7\) (7 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5), nhưng do ta cần tìm đường đi ngắn nhất từ A đến C nên ta ưu tiên khoanh tròn đỉnh C (đỉnh gần A thứ tư).
– Nhìn lại các bước trên, ta thấy:
\(\begin{array}{*{20}{l}}{{n_C}\; = {\rm{ }}5{\rm{ }} = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{l_{AEFC}}.}\end{array}\)
Vậy AEFC là đường đi ngắn nhất từ A đến C, với độ dài bằng 5.
Do đó ta chọn phương án B.
Bài 5 trang 67 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo thường tập trung vào một trong các chủ đề chính của chương trình, ví dụ như hàm số, phương trình, bất phương trình, hoặc các kiến thức về lượng giác. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này bao gồm việc xác định các dữ kiện đã cho, các đại lượng cần tìm, và các điều kiện ràng buộc. Việc phân tích đề bài một cách cẩn thận sẽ giúp học sinh tránh được những sai sót không đáng có và tìm ra hướng giải quyết phù hợp.
Sau khi đã phân tích đề bài, học sinh cần áp dụng các kiến thức và công thức đã học để giải quyết bài toán. Điều này có thể bao gồm việc sử dụng các định nghĩa, định lý, công thức tính toán, hoặc các phương pháp giải đặc biệt. Trong quá trình áp dụng kiến thức, học sinh cần chú ý đến việc lựa chọn công thức và phương pháp phù hợp với từng bài toán cụ thể.
Để giúp học sinh hiểu rõ hơn về cách giải bài 5 trang 67, chúng ta sẽ cùng xem xét một ví dụ minh họa cụ thể. Giả sử bài toán yêu cầu tìm tập xác định của hàm số f(x) = √(x - 2) / (x + 1).
Lời giải này cho thấy tầm quan trọng của việc nắm vững các điều kiện xác định của hàm số và khả năng giải bất phương trình và phương trình. Học sinh cần luyện tập thường xuyên để có thể áp dụng các kiến thức này một cách linh hoạt và hiệu quả.
Ngoài ví dụ minh họa trên, bài 5 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo có thể xuất hiện nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số, phương trình, bất phương trình, và lượng giác. Ngoài ra, học sinh cũng cần luyện tập thường xuyên để có thể áp dụng các kiến thức này một cách linh hoạt và hiệu quả.
Trong quá trình giải bài tập, học sinh cần lưu ý một số điều sau:
Bài 5 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chương trình. Bằng cách phân tích đề bài, áp dụng kiến thức, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập và nắm vững kiến thức Toán 11. Giaitoan.edu.vn hy vọng rằng những hướng dẫn chi tiết và dễ hiểu trên sẽ giúp các em học tập tốt hơn.