Bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 29, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
Đề bài
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
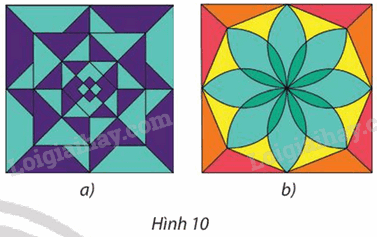
Phương pháp giải - Xem chi tiết
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
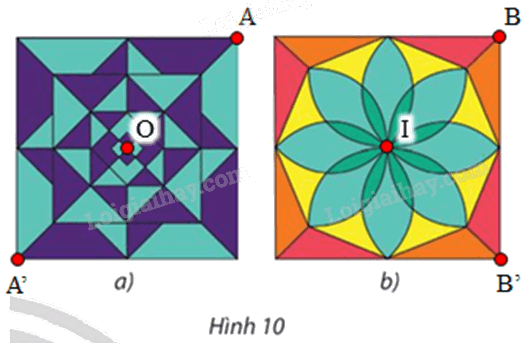
⦁ Hình 10a:
Hình vẽ có dạng hình vuông, gọi O là tâm hình vuông đó và A là 1 đỉnh của hình vuông.
Phép quay tâm O, góc quay 180° biến điểm A thành điểm A’.
Tương tự, ta chọn các điểm khác bất kì trên Hình 10a.
Khi đó qua phép quay tâm O, góc quay 180° ta cũng xác định được ảnh của các điểm đó trên Hình 10a ban đầu.
Vậy phép quay biến Hình 10a thành chính nó là phép quay tâm O, góc quay 180°.
Ngoài ra, phép quay tâm O, góc quay –180° cũng biến Hình 10a thành chính nó.
⦁ Hình 10b:
Hình vẽ có dạng hình vuông, gọi I là tâm hình vuông đó và B là 1 đỉnh của hình vuông.
Phép quay tâm I, góc quay 90° biến điểm B thành điểm B’.
Tương tự, ta chọn các điểm khác bất kì trên hình 10b.
Khi đó qua phép quay tâm I, góc quay 90° ta cũng xác định được ảnh của các điểm đó trên Hình 10b ban đầu.
Vậy phép quay biến Hình 10b thành chính nó là phép quay tâm I, góc quay 90°.
Chú ý: Có nhiều phép quay biến Hình 10a thành chính nó, chẳng hạn ngoài phép quay ở trên, ta có thể kể đến phép quay tâm I, góc quay 180° hoặc phép quay tâm I, góc quay –90°, …
Bài 4 trang 29 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của một đại lượng. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, đề bài sẽ cung cấp một hàm số hoặc một tình huống thực tế, và yêu cầu tính đạo hàm, tìm cực trị, hoặc giải các bài toán tối ưu hóa.
Để giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta có thể áp dụng các phương pháp sau:
(Phần này sẽ trình bày lời giải chi tiết của bài 4 trang 29, bao gồm các bước tính toán, giải thích rõ ràng và kết luận.)
Để giúp các em hiểu rõ hơn về phương pháp giải, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm cực trị của hàm số.
Giải:
Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm trong giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.